カイ二乗検定

＊本サイトのサンプルデータは全て架空のものです

独立性の検定
ｶｲ二乗値とｶｲ二乗分布
- ｶｲ二乗値の求め方

独立性の検定

「独立している」とは？

リハビリテーション研究でよくみかけるカイ二乗検定は、この独立性の検定がほとんどです.

要因 $A_i$ {$i=1, 2, 3$}
要因 $B_j$ {$j=1, 2, 3$}

要因 $A_i$ と要因 $B_j$ が完全に独立している例

df1 <- matrix(c(1, 2, 6, 2, 4, 12, 5, 10, 30), 3, 3)
colnames(df1) <- c("A1", "A2", "A3")
rownames(df1) <- c("B1", "B2", "B3")
#View(df1)

要因Aのレベル（A1, A2, A3）間の比率は、要因Bのレベル（B1, B2, B3）にかかわらず一定で、1:2:5を保っています。この一定の比率は、要因Aと要因Bが互いに独立していることを示唆しており、一方の要因のレベルが他方の結果に影響を与えないことを意味します。つまり、要因Aと要因Bとの間には関連性がないと統計学的に言えます。

$P(A_i∩B_j)＝P(A_i)∗P(B_j)$

この式は、確率論において、二つの事象 $A_i$ と $B_j$ が独立であるということを表しています。すなわち、事象 $A_i$ と事象 $B_j$ が同時に起こる確率 $(A_i∩B_j)$ が、事象 $A_i$ の単独で起こる確率 $P(A_i)$ と事象 $B_j$ の単独で起こる確率 $P(B_j)$ の積と等しい場合、これらの事象は統計学的に独立であると言えます。

独立していない極端な例

df2 <- matrix(c(1, 0, 0, 0, 4, 0, 0, 0, 30), 3, 3)
colnames(df2) <- c("A4", "A5", "A6")
rownames(df2) <- c("B4", "B5", "B6")
#View(df2)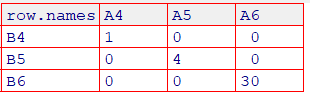

要因 $B4：B5：B6$ の比率は、要因 $A_4, A_5, A_6$ ごとにそれぞれ異なる割合になっています. このような場合には、要因 $B_j$ は要因 $A_i$ に依存しているので、要因 $B_j$ と要因 $A_i$ には何らかの関連性があると考えます. 統計学的な関連性の検証には独立性の検定が用いられ、p値が低ければ $A_i$ と $B_j$ の間に統計的に有意な関連性があることを示唆します. サンプルサイズが小さい場合やデータが2×2の表である場合には、Fisherの正確検定が適切な方法であり、これもまた統計的に関連性があるかどうかを判定するものです.

独立性の検定の帰無仮説

独立性の検定の帰無仮説には、つぎのような表現が使われます(どれも同じ意味です)

事象 $A_i$ と事象 $B_j$ には有意な連関がない
事象 $A_i$ と事象 $B_j$ は独立である
$A_1, A_2, …, A_i$ の割合（比）はどの $B_j$ に対しても共通である
全ての ${}_i{}_j$ に対して $P(A_i∩B_j)＝P(A_i)∗P(B_j)$

サンプルファイル（csvファイルの読み込み方）

kaijijou_01

dat <- read.csv("kaijijou_01.csv", header=T, fileEncoding = "Shift-JIS")

どんなデータフレームになっているか確認してみます
先頭から６行のみ抜き出し

head(dat)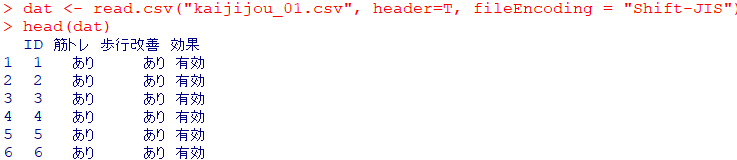

ここまでできればデータの読み込みは完了

datという文字の中にkaijijou_01というエクセルのファイルが読み込まれました. ここからエクセルファイルは直接使わずに、Rで作業を進めていきます.

２変数の分割表の作成

tab <- xtabs(~ 筋トレ + 歩行改善, data = dat)
print(tab)

今度はtabという文字の中に、以下のような分割表が生成されたはずです. tabと入力してEnterキーを押してください. エクセルの一覧表が一気に分割表になります. これでカイ二乗検定の準備完了. あとは以下のように書けば独立性の検定結果を出力してくれます. 有意水準5％で検定してみましょう.

Yates（イエーツ）の補正なし

Yatesの補正なしのカイ二乗検定. この場合はcorrect = FALSEと入力します.

chisq.test(tab, correct = FALSE)

検定結果のみが必要な方は、ここまででOKです. もう少し勉強したい人は次に進みましょう.

Yates（イエーツ）の補正

Yatesの補正は、観測度数と期待度数の差の絶対値から0.5を引いたものを2乗し、期待度数で割ることでカイ二乗統計量を計算します. 特にサンプルサイズが小さい場合に適用されます. この補正は、統計量を低く見積もることがあり、「イエーツの補正は過剰に保守的である」との意見もあります. サンプルサイズが小さく、特に期待度数が5以下のセルが含まれる場合には、カイ二乗検定よりもフィッシャーの正確確率検定の方が適切な場合があります.

Yates（イエーツ）の補正を加えたカイ二乗検定

chisq.test(tab)

RはYatesの補正がデフォルト設定になっています

p < 0.05なので、筋トレと歩行改善は『独立していない』という結果になりました. つまり、筋トレの有無と歩行練習の有無には何らかの関連性があるということです. yatesの補正はカイ二乗値が小さくなるような補正ですのでｐ値が大きくなります.

ｶｲ二乗値とｶｲ二乗分布

ｶｲ二乗値の求め方

ｶｲ二乗検定の統計量 ( X-squared = 6.0764 ) となる、ｶｲ二乗値は以下のようにして求めます

$\sum\sum\dfrac{(観測度数 – 期待度数)^2}{期待度数}$

ちなみにYatesの補正をした場合の統計量は以下のようになります

$\sum\sum\dfrac{(|観測度数 – 期待度数|-0.5)^2}{期待度数}$

ｶｲ二乗値を直接求めてみましょう！

addmargins(tab)

いかのような出力になったでしょうか（分割表の周辺和が出るはずです）

患側度数と期待度数を求めてｶｲ二乗値を求めます

期待度数

20*20/35
20*15/35
15*20/35
15*15/35

ｶｲ二乗値

((15-20*20/35)^2)/(20*20/35) +
((5-20*15/35)^2)/(20*15/35) +
((5-15*20/35)^2)/(15*20/35) +
((10-15*15/35)^2)/(15*15/35)

ｶｲ二乗値は以下のようになったでしょうか？

上で求めたX-squared = 6.0764と同じ値になりました

yatesの補正をした場合のｶｲ二乗値 (X-squared = 4.4941) も求めてみましょう

((abs(15-20*20/35)-0.5)^2)/(20*20/35) +
((abs(5-20*15/35)-0.5)^2)/(20*15/35) +
((abs(5-15*20/35)-0.5)^2)/(15*20/35) +
((abs(10-15*15/35)-0.5)^2)/(15*15/35)

chisq.test関数で求めた統計量と同じ値になりました