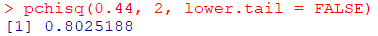カイ二乗分布
自由度1のカイ二乗分布
R
curve(dchisq(x, 1), xlim=c(0, 8), ylim=c(0, 1))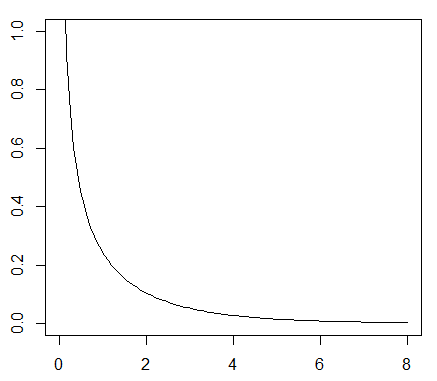
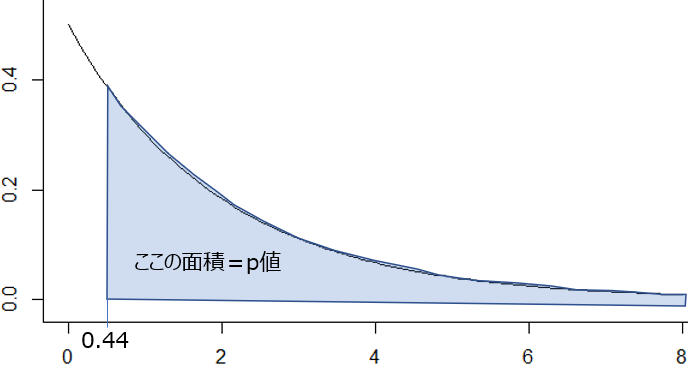
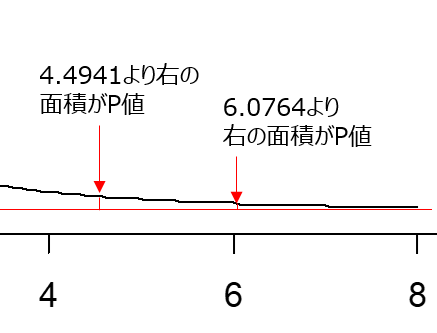
このような図が描けたでしょうか?これが自由度1のカイ二乗分布です. dchisq(x, 1) の数字の部分が自由度ですのでdchisq(x, 2) に変更すると自由度2のカイ二乗分布が描けます. カイ二乗値が 6.0764 なのでかなり右裾に位置することが理解できます. Yatesの補正の場合は分子から0.5を引いているのでカイ二乗値は小さくなり、4.4941 という値だったので、P値が大きくなることが理解できます.
適合度の検定
本来であれば独立性の検定の前に書くべきでしょうが、リハビリテーション研究にはあまり利用されておりませんので、後に回しました。
どんな検定か?
理論上の確率分布から得られる期待度数 (Expected frequency) を求めることが前提となります.その期待度数を利用して観測度数 (Observed frequency) が適合するかどうか(当てはまりの良さ)を検定します.
適合度の検定の帰無仮説
・各カテゴリーにおける観測された割合は、それぞれのカテゴリーに期待される割合と同じである.
・各階級の発生確率は、想定される母集団分布の確率と同じである.
・観測されたデータの分布は、想定される理論的確率分布に従っている.
例)次のデータはメンデルの法則 1:2:1 の確率に適合しているか?
R
観測度数 <-c( 52, 102, 46 )
理論確率 <- c ( 1/4, 1/2, 1/4 )
遺伝子 <- c("AA", "Aa", "aa")
tab <- data.frame(遺伝子, 観測度数, 理論確率)
#View(t(tab))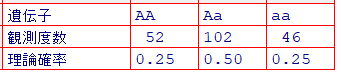
R
chisq.test(観測度数, p=理論確率) 
帰無仮説は棄却されないので、理論確立に従っていることが証明されました
期待度数は、次のように計算します(理論確立があるので簡単です)
R
期待度数 <- 理論確率*sum(観測度数)
print(期待度数)
観測度数と期待度数は以下のようになります
R
観測度数 <-c(52, 102, 46)
期待度数 <- c (50, 100, 50)
遺伝子 <- c("AA", "Aa", "aa")
tab2 <- data.frame(遺伝子, 観測度数, 期待度数)
#View(t(tab2))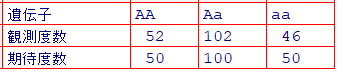
カイ二乗値の求め方は独立性の検定と同じです
$\sum\sum\dfrac{(観測度数 – 期待度数)^2}{期待度数}$
R
(52-50)^2/50 + (102-100)^2/100 + (46-50)^2/50
カイ二乗分布は自由度2なので以下のようなグラフになります
R
curve(dchisq(x, 2), xlim = c(0, 8), ylim = c(0, 0.5))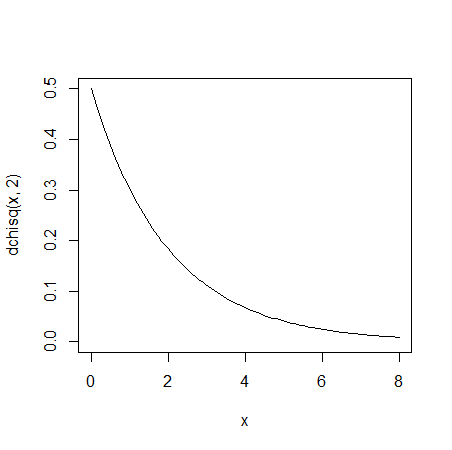
Rを使用してカイ二乗値からp値を求める場合は・・・
R
pchisq(0.44, 2, lower.tail = FALSE)