ポアソン分布

確率関数

単位時間に平均 $\lambda$ 回起こることが、ある期間で $k$ 回おこる確率の分布

確率関数: $P(X=k)=$ $\frac{e^{-\lambda }{\lambda }^k}{k!}$

期待値: $\lambda$

分散: $\lambda$

• ある場所での交通事故の発生数
• ある製品の不良品の発生数
• １時間あたりの病気の発症数
• １日にかかる電話の本数

次の例題は僕が考えた架空のものです

例題 ($\lambda =5,k=1)$

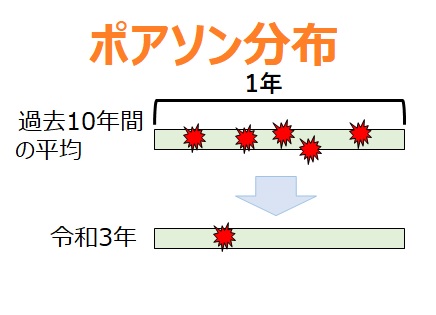
単位時間を1年間として、発生頻度が5回/年を例として考えます

施設Aの過去10年間のデータから、5回/年の転倒事故が起こっていることが分かりました

転倒防止委員会を立ち上げ対策を講じた結果、令和3年の施設Aの転倒回数が1回/年に減少しました

この施設で、転倒頻度が1回/年となる確率はどれくらいでしょうか？

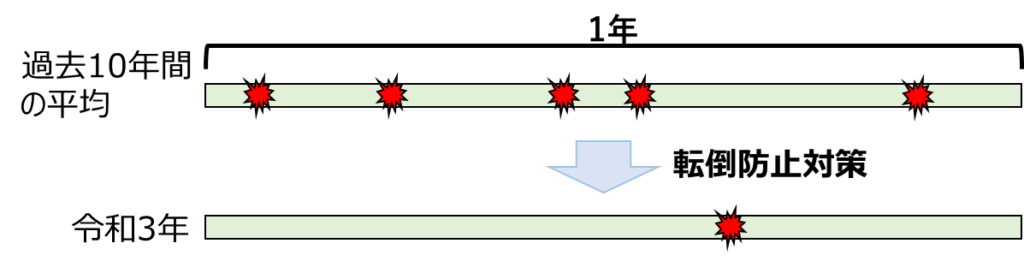
転倒頻度が1回/年となる確率が低ければ、転倒防止対策の効果として考えてみてもよいかもしれません

ポアソン分布を使用することで、この確率を求めることができます

$\lambda$ は1年間に起こる平均回数（5回）

$k$ は令和3年に起きた1回（確率を求めたい単位時間の回数）

次の関数から年1回の転倒が起きる確率を求めることができます

$P(X=1)=$ $\frac{e^{-5}{5}^1}{1!}$ $=0.03368973$

確率3.4%という結果ですので、転倒防止策の効果はあったのかもしれませんね（実際の調査では交絡因子を探り当てて因果関係を考察します）

Rで求めてみましょう

二項分布とは異なり、ポアソン分布に必要なパラメーターは「回数」のみです

つまり１と5を与えることで確率が算出されます

dpois(x = 1, lambda = 5)

当たり前ですが答えは同じです

0.03368973

やはり便利ですね

この例の確率分布は以下のようになります

t <- 0:12
p <- dpois(x = t, lambda = 5) #bが入るので注意（これは英語の勉強です）
barplot(p ~ t, pch = 16, xlab = "", ylab = "")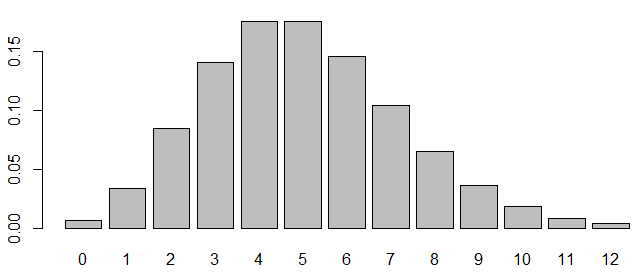

二項分布

ポアソン分布は二項分布と似ていますね

ポアソン分布は、「2種類の結果（0または1）の値をとる独立した試行で、確率が低く試行回数が非常に多い場合の1が得られる回数の確率分布」と言えます

１年を12ヶ月として、「12回中に何回起きるか」という問題に置き換えると二項分布として考えることができます

確率は 5 ÷ 12 ≒ 0.42

$P(X=k)={}_{12}{C}_k{0.42}^k(1-0.42{)}^{12-k}$

t <- 0:12
p <- dbinom(x = t, size = 12, prob = 5/12)
barplot(p ~ t,  pch = 16, xlab = "", ylab = "")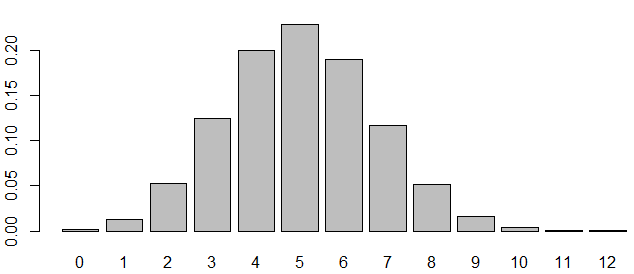

なんとなくポアソン分布に似ています

次に１年を365日（365回）と置き換えた場合の二項分布です

確率は 5 ÷ 365 ≒ 0.014

$P(X=k)={}_{365}{C}_k{0.014}^k(1-0.014{)}^{365-k}$

t <- 0:12
p <- dbinom(x = t, size = 365, prob = 5/365)
barplot(p ~ t,  pch = 16, xlab = "", ylab = "")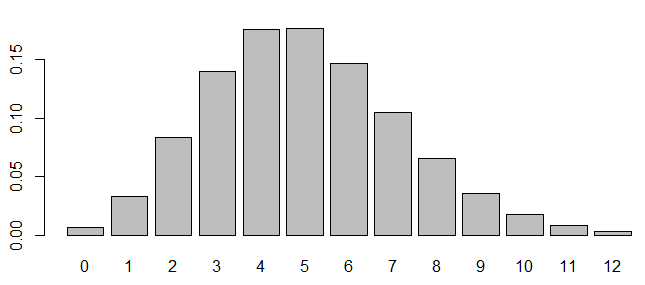

二項分布とポアソン分布がほぼ同じ分布を示しています

このように試行回数が多く、かつ確率が低い場合には、以下の法則が成立します

ポアソンの極限定理（ポアソン分布は二項分布の極限）

二項分布の期待値 $np=\lambda$ を固定した状態で$ｎ\to \infty$にすることでポアソン分布が導出されます（この場合、必然的に$\pi \to 0$となります）

$np=\lambda$ を条件とした場合、${\displaystyle \underset{n\to \mathrm{\infty }}{lim}{}_n{C}_k{\pi }^k(1-\pi {)}^{n-k}=\frac{e^{-\lambda }{\lambda }^k}{k!}}$

証明を知りたい人は鉄板サイトヨビノリのポアソン分布で勉強しましょう

• ポアソン分布は、$\pi \to 0$なので二項分布とは異なり稀に起きる現象です
• パラメータは「事象回数のみ」という特徴があり、調査期間が長く発生頻度が低い場合に適しています
• サイズ $ｎ$ が大きく、確率 $\pi$ が小さい二項分布の近似として利用できます

参考文献

• 統計学入門 (基礎統計学Ⅰ), ISBN-10: 9784130420655
• Rとグラフで実感する生命科学のための統計入門, ISBN-10: 475812079X
• 改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎, ISBN-10 ‏ : ‎ 4489022271