Fisherの正確確率検定

間違った解釈をしないように！

再掲

	効果あり	効果なし	計
重度群	12	3	15
軽度群	6	8	14
合計	18	11	29

AM実施群が有効であることを証明したい場合

帰無仮説H0: AM群の効果率＝ PM群の効果率
対立仮説H1: AM群の効果率＞ AM群の効果率

上記のような実験結果から試験群の有効率が対照群の有効率より大きいことを証明します．
Fisherの直接法により有意水準5%で検定しましょう．

tab <- matrix(c(12, 6, 3, 8), 2, 2)
fisher.test(tab)

p=0.06となり有意差はありません・・・
という回答は間違っています．

fisher.testのデフォルトを確認しましょう

?fisher.test

alternative = “two.sided”
両側検定が初期設定として機能しています．
しかし今回の検定は「片側検定を5％水準で行う」と宣言しています．
alternative = “less“または“greater”を設定しなければなりません．
さてどちらを選択すればよいでしょうか・・・？

“less“

先に述べましたようにX≦12となる確率算出します．
p-value = 0.9935

Rは分割表の左上を基準にしています

たまたまAM実施群の効果ありが左上にあるので、そこが基準となっています

それでは左列が効果なしなっている分割表に換えてみましょう

# c(2, 1) 2列目と1列目を入れ替えるという指示です
tab2 <- tab[, c(2, 1)] 
tab2

これで列が入れ替わりました

検定してみましょう

fisher.test(
    tab2, alternative = "less"
    )

fisher.test(
tab, alternative = “less”
)

のときはp-value = 0.9935でしたが

fisher.test(
tab2, alternative = “less”
)

ではp-value = 0.04601となっています．

なので…基準を間違うと検定結果も間違うということになります．

今回は「 AM実施が有効＞ PM実施が有効」を証明したいので・・・

tab2のまま検定するのであれば、

fisher.test(
tab2, alternative = “less“
)

tabで検定するのであれば

fisher.test(
tab, alternative = “greater“
)

ということになります

もちろんどちらも同じｐ値になります
＊ただし分割表の基準が異なるのでオッズ比も異なります

3群以上の場合

帰無仮説：3群における効果率は等しい
対立仮説：3群における効果率は等しくない（3群のどこかで効果率が異なる）
または
帰無仮説：クラメールの連関係数 = 0
対立仮説：クラメールの連関係数 > 0

要するにｶｲ二乗検定の独立性の検定です・・・

tab3 <- matrix(c(15, 12, 6, 3, 3, 10), 3, 2)
tab3

以下のような分割表を検定してみます

Z法の効果	効果あり	効果なし	計
重度群	12	3	15
中等度群	21	28	49
軽度群	6	8	14
合計	29	13	42

fisherの正確検定

fisher.test(tab3)

fisherの正確検定は大変複雑な計算になりますが、Rでは一瞬で算出してくれます。両側検定をした結果は、p=0.048 となり統計学的に効果率には差があるという結果になりました。

fisher.test(tab3, alternative = "less")
fisher.test(tab3, alternative = "greater")

３群以上の場合は、３群の割合の差の二乗の和が0か0じゃないかの検定なので、片側検定の意味はありません。なので上記のように片側検定を行っても同じ答えになります。

ｶｲ二乗検定も同様ですが、３群以上のFisherの正確検定は、3群における効果の有無に差があるかどうかを検定しています。以下、ｶｲ二乗検定の結果です。

ｶｲ二乗検定

chisq.test(tab3)

p値は少し異なりますが、ｶｲ二乗検定もやはり有意として答えてくれません。

fisherの正確検定、ｶｲ二乗検定ともに３群の効果率には違いがあるという結果になりました。計算は非常に面倒なことになるので（2✕2分割表でも大変でした）、他の参考書などをご参照ください。

多重比較

グループ間の割合に差があるということなので、多重比較を行う場合が多いと思われます。でも、個人的には井口先生のご意見に賛成です。以下をご参照ください。

Fisher 正確検定の後に多重比較するな

...

このことを理解した上で、一応多重比較の方法のみ記載しておきます。
使用するパッケージは、RVAideMemoire

インストールしてない場合は

install.packages(“RVAideMemoire”)

library(RVAideMemoire)

以下のようなｐ値調整の方法があります

ホルム

実際にやってみましょう
A=１行目、B＝2行目、C＝３行目

#ホルム
fisher.multcomp(tab3, p.method="holm")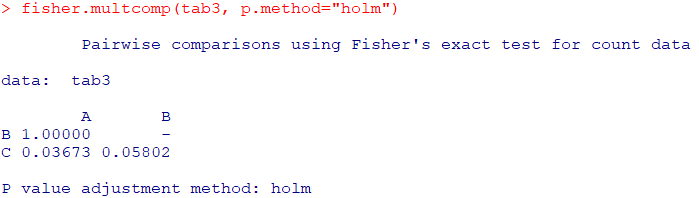

ボンフェローニ

#ボンフェローニ
fisher.multcomp(tab3, p.method="bonferroni")

どちらの方法も１行目と3行目に有意差ありという判定でした。