
指数分布
- 指数分布はイベント発生までの待ち時間の分布です(生物統計学における生存時間、システムが故障すまでの時間など)
- 無記憶性(一番下で解説)という性質をもつため、以前のイベント発生に関係なく初めてのイベント発生までの待ち時間の分布を示します
- ちなみにポアソン分布は一定時間内に生起する回数の分布です
確率関数
\(\lambda\) はある単位時間内のイベント発生数
\(t\) は待ち時間(単位を1時間とする場合は、15分は0.25となる)
確率密度関数:\(
\begin{equation}
f(x) = \left\{
\begin{alignedat}{2}
\lambda e^{-\lambda t} \quad (t \geq 0) \\
0 \quad (t<0)
\end{alignedat}
\right.
\end{equation}
\)
累積分布関数:\(F(t)=P(X \leq t)=1-e^{- \lambda t}\)
期待値:\(\dfrac{1}{\lambda}\)
分散:\(\dfrac{1}{\lambda^2}\)
\(\lambda\) により分布がきまるので\(Ex(\lambda)\) または \(Exp(\lambda)\) と標記される
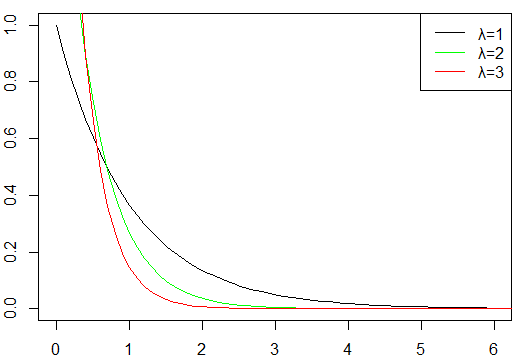
#グラフ
x <- seq(0, 10, length = 100)
data <- data.frame(
l1 = c(exp(-1*x)),
l2 = c(2*exp(-2*x)),
l3 = c(3*exp(-3*x))
)
cols <- c("black", "green", "red")
ltys <- c(1, 1, 1)
plot(
0, 0, type = "n",
xlim = c(0, 6), ylim = c(0, 1),
xlab = "", ylab = ""
)
for (i in 1:ncol(data)) {
lines(x, data[, i], lty = ltys[i], col = cols[i])
}
legend(
"topright",
legend = c("λ=1", "λ=2", "λ=3"),
col = cols,
lty="solid"
)
トレーニングマシーンの故障に関する例題です。ここでは、1単位を10年とします。つまり10年=1となります。
例題
あるトレーニング機器の故障頻度は10年に1回と報告されています。この医療機器が5年以内に故障する確率はどれくらいになるでしょうか。待ち時間が5年以内の確率ということになります。5年以内なので故障する確率は低いと思うのですが・・・。
\(\lambda=1\)
\(t=\dfrac{5}{10}=0.5\)
累積分布関数から確率を求める
\(F(t)=P(X \leq t)=1-e^{- \lambda t}\) に当てはめる
\(F(0.5)=P(X \leq 0.5)\)
\( \, =1-e^{- 1 \times 0.5}=0.3934693\)
1 - exp(-1*0.5)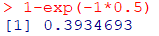
約40%の確率でこのマシーンが故障がするこが予測されました.累積分布関数のグラフから待ち時間が長くなるとイベント発生の確率が高くなること、また徐々に上昇率が低くなることが理解できます.
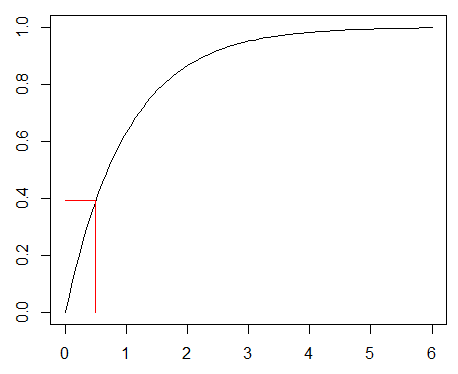
#グラフ
t <- seq(0, 6, length = 100)
y <- c(1 - exp(-1*t))
plot(
t, y, type = "l",
xlim = c(0, 6), ylim = c(0, 1),
xlab = "", ylab = ""
)
lines(
c(0.5, 0.5, 0),
c(0, 1 - exp(-0.5*1), 1 - exp(-0.5*1)),
col = "red"
)確率密度関数から確率を求める
pexp(q = 0.5, rate = 1)
0で確率が非常に高くなるのは、イベントが発生していない確率が非常に高いからです
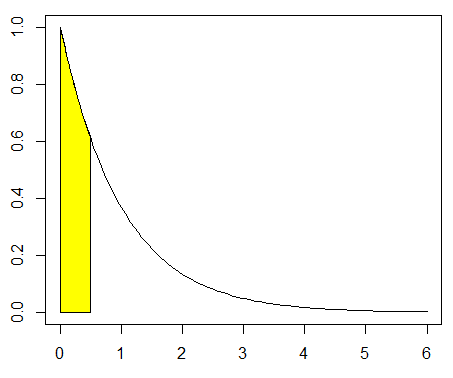
#グラフ
t <- seq(0, 6, length = 100)
y <- c(1*exp(-1*t))
plot(
t, y, type = "l",
xlim = c(0, 6), ylim = c(0, 1),
xlab = "", ylab = ""
)
x <- seq(0, 0.5, length = 100)
y <- c(1*exp(-1*x))
polygon(
c(x, rev(x)),
c(rep(0, length(x)), rev(y)),
col = "yellow"
)指数分布の無記憶性
\(P(X>s+t \,|\, X>s) \)
\(=\dfrac{P(X>s+t \, , \, X>s)}{P(X>s)}\)
\(= \dfrac{e^{-\lambda(s+t)}}{e^{-\lambda s}}\)
\(= e^{-\lambda t}\)
\(= P(X>t)\) \(\qquad s>0, \,t>0\)

sをある時点として説明します.「ある時点s以降におけるイベント発生までの待ち時間がtより長くなる確率は、時点sまでのイベント発生待ち時間には関係なくtの値で決まる」という意味になります.簡単に言うと「指数分布は、以前のイベント発生に依存せず、次のイベントが起こる待ち時間の分布」ということになります.
指数分布は、前のエベント発生に影響されません.「先週まで転倒事故(イベント)が発生してないので、今週も転倒事故はないだろう」とは言えません.このような場合の転倒予測などに使用される確率分布になります.無記憶性をもつ,連続的なモデルを扱いたい場合は,指数分布を用いることになるでしょう.
参考サイト
証明などの詳細は下記のブログを参照ください
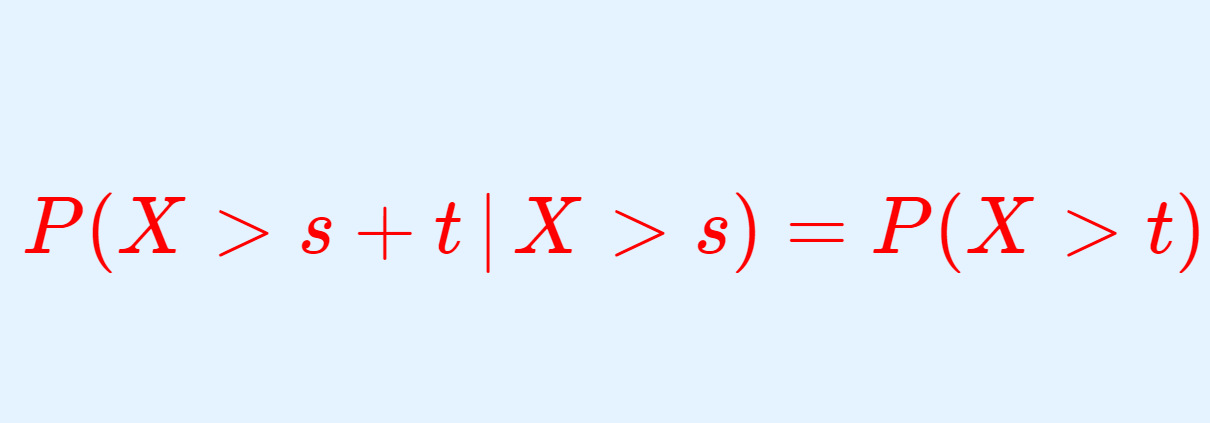

コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください