比率の差の検定（リハビリ回数の満足度調査）

正規分布を利用した検定

両グループの母集団から得られた確率変数\(X1, X2\)が二項分布に従う場合

\(X1 \sim B(n1, \pi1)\), \(X2 \sim B(n2, \pi2)\)

\(n_1, n_2\)が大きい場合、標本比率は正規分布に従う（大数の法則）

\(\hat{\pi}1-\hat{\pi}2 \sim N(\pi1-\pi2, \frac{\pi1(1-\pi1)}{n1}+\frac{\pi2(1-\pi2)}{n2})\)

zが標準正規分布に従うことを利用して検定を行う

\(\displaystyle z=\frac{(\hat{\pi}1-\hat{\pi}2)-(\pi1-\pi2)}{\sqrt{\frac{\hat{\pi}1(1-\hat{\pi}1)}{n1}+\frac{\hat{\pi}2(1-\hat{\pi}2)}{n2}}}\)

したがって、2つのサンプルの比率 \(\frac{116}{192}, \frac{244}{288}\) の母比率差も正規分布となります

\(\hat{\pi}_1-\hat{\pi}_2 \sim N(\pi_1-\pi_2,\frac{\pi_1(1-\pi_1)}{n_1}-\frac{\pi_2(1-\pi_2)}{n_2})\)

以下の統計量Zが正規分布(平均0、分散1の標準正規分布)に従うことを利用します

\(\displaystyle z=\frac{(\hat{\pi}_1-\hat{\pi}_2)-(\pi_1-\pi_2)}{\sqrt{\frac{\hat{\pi}_1(1-\hat{\pi}_1)}{n_1}+\frac{\hat{\pi}_2(1-\hat{\pi}_2)}{n_2}}}\)

確率変数の分散の加法性
XとYが独立である場合　V(X ± Y)=V(X) + V(Y)

帰無仮説は \(\pi_1=\pi_2\) なので \(\pi_1-\pi_2=0\) の場合のｚ値を求めす

#週4回満足
a1 <- 116
#週4回不満 
a2 <- 76
#週4回のn
n1 <- a1 + a2
#週5回満足
b1 <- 244
#週5回不満
b2 <- 44
#週5回のn
n2 <- b1 + b2
pi1 <- a1 / n1
pi2 <- b1 / n2
#Z値
z <- (pi2 - pi1) / sqrt((pi1 * (1 - pi1) / n1) + (pi2 * (1 - pi2) / n2)))
print(z)

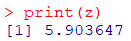
Z値 = 5.9 > 1.96 となるため帰無仮説は棄却されます（結論はｶｲ二乗検定と同じですね）

curve(dnorm(x), type = "l", ylim = c(0, 0.5), xlim = c(-4, 4))
x <- qnorm(0.025, lower.tail = FALSE) #これがZ値です
x1 <- seq(x, 5, length = 100)
y <- dnorm(x1)
polygon(c(x1, rev(x1)), c(rep(0, length(x1)), rev(y)), col = "pink")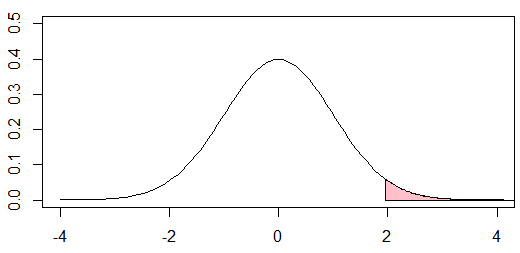

1.96はｐ＝0.025(ピンク色の部分)のときのＺ値（x軸）です

95％信頼区間の求め方

正規分布を利用して信頼区間を算出します

\(\displaystyle z=\frac{(\hat{\pi}_1-\hat{\pi}_2)-(\pi_1-\pi_2)}{\sqrt{\frac{\hat{\pi}_1(1-\hat{\pi}_1)}{n_1}+\frac{\hat{\pi}_2(1-\hat{\pi}_2)}{n_2}}}\)

\(\displaystyle \pi_1-\pi_2=(\hat{\pi}_1-\hat{\pi}_2)\pm{z}(\sqrt{\frac{\hat{\pi}_1(1-\hat{\pi}_1)}{n_1}+\frac{\hat{\pi}_2(1-\hat{\pi}_2)}{n_2}})\)

z <- qnorm(0.025)
def <- (116 / 192) - (244 / 288)
denominator <- sqrt((116 / 192) * (1 - 116 / 192) / 192 + (244 / 288) * (1 - 244 / 288) / 288)
confidence_interval <- numerator + c(1, -1) * z * denominator
print(confidence_interval)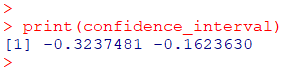

参考文献

改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎（ISBN978-4-489-02227-2 C3040）