
t分布
母集団の分散が未知の場合に、標本不偏分散を使用したt分布により区間推定を行います
自由度(\(n-1\))のt分布
\(t=\dfrac{\bar{X}-\mu}{\sqrt{\dfrac{s^2}{n}}}\)
よって
\(\mu = \bar{X} \pm t\sqrt{\dfrac{s^2}{n}}\)
Rの関数t.testで95%信頼区間を求める
例題
地域Aに在住する5~7歳の痙直型両麻痺児(GMFCSレベルⅢ)10名の背臥位から割座までの起き上がり時間を測定した。結果は、5.8, 9.5, 8.5, 10.6, 9.6, 13.5, 11.5, 9.3, 6.6, 8.3となりました。90%の信頼度で母平均を推定(90%信頼区間)してみましょう。
Rのt検定の関数で求めてみましょう
R
t.test(dat, conf.level = 0.9)
t値を求める
90%信頼区間を求めるために、自由度9のt分布からt値を求めます.Rを使用すると以下のような関数で求めることができます(確率密度関数を積分することで求めることも可能です).
R
qt(0.05, 9)
qt(0.05, 9, lower.tail=F)
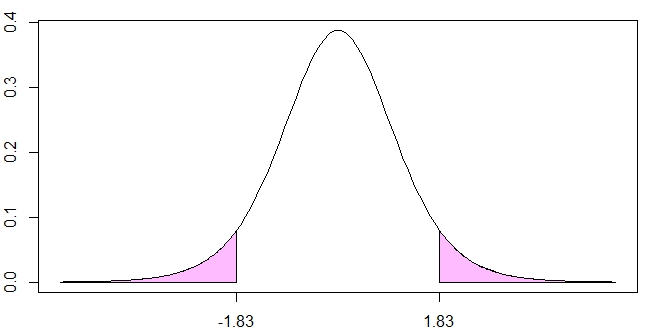
この値がt値となり、下図のピンク色の部分の合計が0.1となっています
R
#グラフ
xseq <- seq(-5, 5,length=100)
plot(xseq, dt(xseq, 9),type="l", xaxt="n")
p <- seq(qt(0.05, 9, lower.tail=F), 5, length=100)
y <- dt(p, 9)
polygon(c(p,rev(p)), c(rep(0,length(p)), rev(y)), col="plum1")
p2 <- seq(-5, qt(0.05, 9), length=100)
y <- dt(p2, 9)
polygon(c(p2,rev(p2)), c(rep(0,length(p2)), rev(y)), col="plum1")
axis(side=1, at=c(round(qt(0.05, 9),2), round(qt(0.05, 9, lower.tail=F),2)))両端の合計が0.05になるt値を代入することで95%信頼区間も求めることができます
R
qt(0.025, 9)
qt(0.025, 9, lower.tail=F)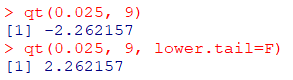
標本平均と不偏分散より95%信頼区間を求める
R
dat <- c(5.8, 9.5, 8.5, 10.6, 9.6, 13.5, 11.5, 9.3, 6.6, 8.3)
mean(dat) #平均
var(dat) #不偏分散
# 注意)Rには標本分散を算出する関数はありません(必要に応じで自力で計算式を書かなければなりません)
90%信頼区間
R
mean(dat)+c(-1, 1)*qt(0.05, 9, lower.tail=F)*sqrt(var(dat)/length(dat))
90%信頼区間は8.02~10.62となりました.結果の解釈については研究計画に応じて異なります.

コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください