両側検定
対立仮説1（\(\mu \neq 0 \)）を有意水準5％で検定してみましょう
自由度9のｔ分布
R
x <- seq(-5, 5, length=100)
plot(
x, dt(x, 9), type = "l",
xlim=c(-5, 5), ylim=c(0, 0.4),
xlab="", ylab="", xaxt="n"
)
t <- mean(sa)/sqrt(var(sa)/length(sa))
lines(c(t, t), c(-1.5, dt(t, 9)))
axis(side=1, at=t)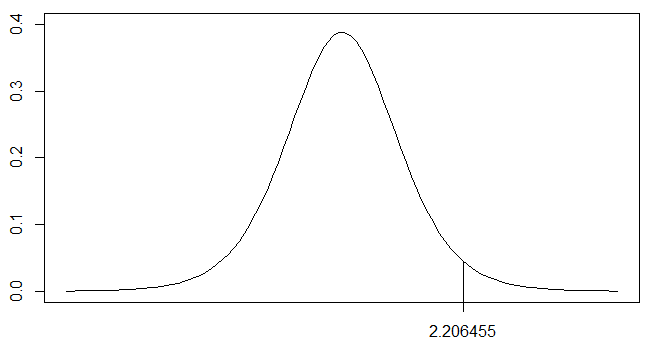
有意水準5%なので右側の面積 $<0.025$ であれば両側検定で帰無仮説が棄却できます．右側の面積が $<0.025$ の部分を青色で塗りつぶしてみましょう．
R
x <- seq(-5, 5, length=100)
plot(
x, dt(x, 9), type = "l",
xlim=c(-5, 5), ylim=c(0, 0.4),
xlab="", ylab="", xaxt="n"
)
q = qt(0.025, 9, lower.tail=F)
p <- seq(q, 5, length=100)
y <- dt(p, 9)
polygon(c(p,rev(p)), c(rep(0,length(p)), rev(y)), col="#72C6EF")
t <- mean(sa)/sqrt(var(sa)/length(sa))
lines(c(t, t), c(-1.5, dt(t, 9)))
axis(side=1, at=t)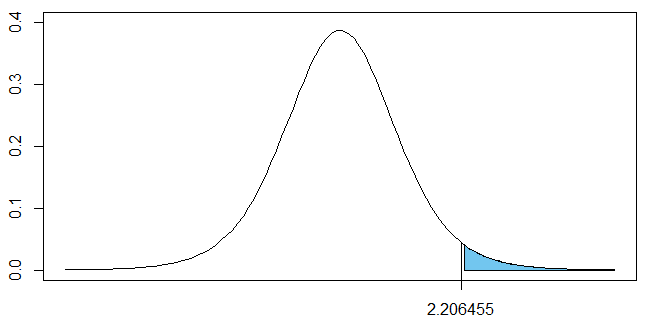
2.21は棄却域には入っていないようなので、ｐ値は0.05より少し大きい値となっていることが予想できます
Rの関数で確認してみましょう
R
t.test(sa)
ｔ値は2.21でｐ値は0.055です．p>0.05で有意差なし・・・という結果になりました．
p値
上記の検定は両側検定でした．したがって求めたp値は両側の裾の面積になります．
R
x <- seq(-5, 5, length=100)
plot(
x, dt(x, 9), type = "l",
xlim=c(-5, 5), ylim=c(0, 0.4),
xlab="", ylab="", xaxt="n"
)
t <- mean(sa)/sqrt(var(sa)/length(sa))
p <- seq(t, 5, length=100)
y <- dt(p, 9)
polygon(c(p,rev(p)), c(rep(0,length(p)), rev(y)), col="yellow")
p2 <- seq(-t, -5, length=100)
y <- dt(p2, 9)
polygon(c(p2,rev(p2)), c(rep(0,length(p2)), rev(y)), col="yellow")
axis(side=1, at=c(-t, t))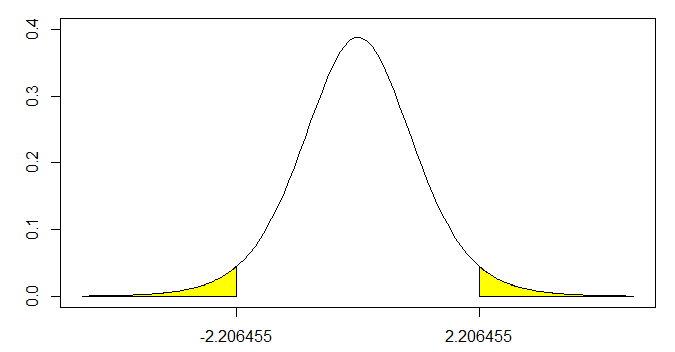
両側検定の場合は、正確には以下のように描かなければなりません．両側の黄色い部分の合計面積が0.05となります．
R
x <- seq(-5, 5, length=100)
plot(
x, dt(x, 9), type = "l",
xlim=c(-5, 5), ylim=c(0, 0.4),
xlab="", ylab="", xaxt="n"
)
q = qt(0.025, 9, lower.tail=F)
p <- seq(q, 5, length=100)
y <- dt(p, 9)
polygon(c(p,rev(p)), c(rep(0,length(p)), rev(y)), col="#72C6EF")
q = qt(0.025, 9, lower.tail=F)
p2 <- seq(-q, -5, length=100)
y <- dt(p2, 9)
polygon(c(p2,rev(p2)), c(rep(0,length(p2)), rev(y)), col="#72C6EF")
lines(c(t, t), c(-1.5, dt(t, 9)))
lines(c(-t, -t), c(-1.5, dt(-t, 9)))
axis(side=1, at=c(-t, t))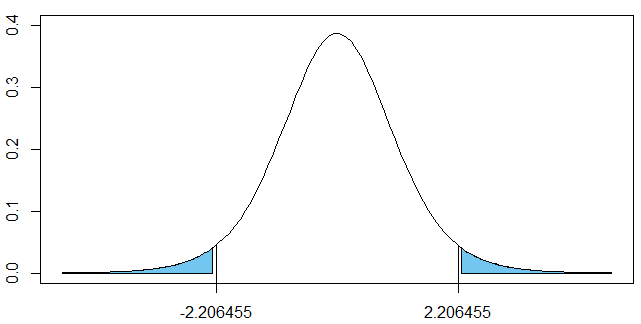
上側検定
post > pre を有意水準5％で証明してみます
対立仮説2：(post – pre）の平均 ＞ 0
t値は両側検定で求めた値と同じです
R
t <- mean(sa)/sqrt(var(sa)/length(sa))
print(t)
これは一側の検定ですの、下のグラフの緑色部分のみがp値として算出されます．つまり両側検定のときの半分のｐ値になります．
R
x <- seq(-5, 5, length=100)
plot(
x, dt(x, 9), type = "l",
xlim=c(-5, 5), ylim=c(0, 0.4),
xlab="", ylab="", xaxt="n"
)
t <- mean(sa)/sqrt(var(sa)/length(sa))
p <- seq(t, 5, length=100)
y <- dt(p, 9)
polygon(c(p,rev(p)), c(rep(0,length(p)), rev(y)), col="yellow")
lines(c(t, t), c(-1.5, dt(t, 9)))
axis(side=1, at=t)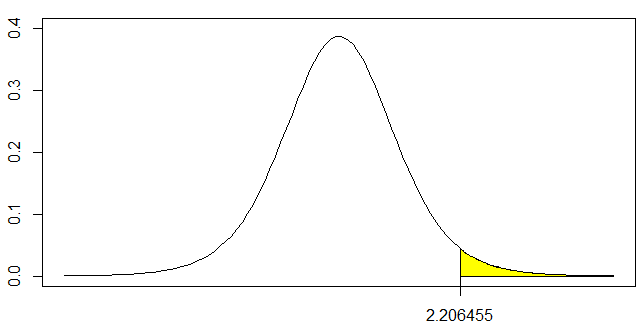
有意差検定を行う場合は、このように統計量とｐ値との関係性をイメージしながら検証されることをお勧めします．その場合、Rは最適なツールになります．同じ有意水準５％でも片側検定だと有意な結果になりました．「統計のマジック・・・」という人もいるかもしれませんが、別にトリックではないので、解析結果を見誤ったりしないように注意が必要ですね．
コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください