対応のあるt検定

1ページ　2ページ

データの準備と要約

僕が作った架空のデータで練習しましょう。結果についてはご意見があると思いますが、統計学の練習のためのサンプルですのでご了承ください。信頼区間の求め方は母平均の区間推定（母分散が未知の場合）をご覧ください。

例題）COPDの男性患者10名を対象にして、入院時と入院2週間後に6分間歩行距離(m)を計測した。両時点での歩行距離に差があるか有意水準5%で検証せよ。

Rを使って10名のサンプルを作成します。計測結果（pre: 入院時、post: 2週間後）。

ID <- 1:10
pre <- c(330, 410, 410, 315, 395, 290, 250, 335, 302, 340)
post <- c(350, 420, 408, 333, 445, 312, 275, 312, 295, 395)
data <- data.frame(ID, pre, post)
head(data)

対応のあるデータのグラフ

x <- c(1.1, 1.9)
data2 <- t(data[,2:3])
print(data2)

グラフ（dat2を使用します）

matplot(
    x, data2,
    type ="b", lty=2,
    xaxt="n", 
    xlim=c(1, 2),
    xlab="", ylab=""
)
name <- c("入院時", "2週間後")
axis(side=1, at=c(1.1, 1.9), labels=name)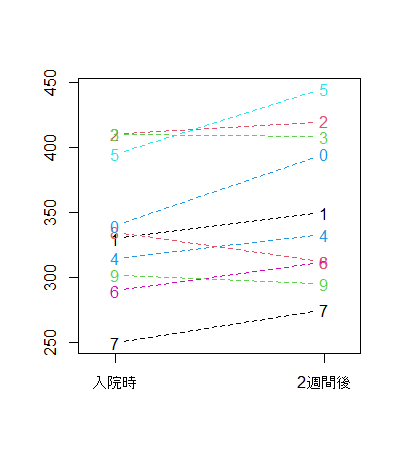

仮説

帰無仮説：入院時の歩行距離と2週間後の歩行距離に差はない\( \quad (pre=post)\)
対立仮説1：入院時と2週間後の歩行距離の差の平均は0ではない\( \quad (pre \neq post)\)
対立仮説2：2週間後の歩行距離は入院時の歩行距離より長い\( \quad (post – pre ＞ 0)\)

対立仮説1を証明する場合には両側検定、対立仮説2を検証する場合には片側検定となります．入院治療の効果を判定する場合には、本来であれば対立仮説2になるのですが、対立仮説1で検証している報告が多いようです．

t検定

仮説1の両側検定

sa <- data$post - data$pre
t.test(sa)

p>0.05で有意差なし・・・という結果になりました

仮説2の片側検定

t.test(sa, alternative="greater")

ｐ＜0.05で有意になりました

結果のみよければ、ここまでです

ここからはもう少し深く勉強してみましょう

統計量

2週間後 – 入院時： \(post-pre\)
（2週間後 – 入院時）の平均値：\(\bar{x}\)
（2週間後 – 入院時）の母平均値：\(\mu\)
（2週間後 – 入院時）の不偏分散: \(s^2\)

# Sample mean
mean(sa)
# Sample unbiased variance
var(sa)

母分散が未知の平均値の差の検定なので、ｔ統計量を使用します   (\(\sim t(10-1)\))．また帰無仮説では \(pre=post\) を仮定しているので \(\mu = 0\) とします．

\(t=
\dfrac{\bar{x}-\mu}{\sqrt{\dfrac{s^2}{n}}}=\dfrac{16.8-0}{\sqrt{\dfrac{579.733}{10}}}\)

標本不偏分散の求め方

$V[A – B] = V[A] + V[B] – 2cov(A, B)$ より

var(data$pre) + var(data$post) - 2*cov(data$pre, data$post)

t値の求め方

t <- mean(sa)/sqrt(var(sa)/length(sa))
print(t)

Rの検定結果に記載してあるｔ統計量と同じ値になりました。この統計量（ｔ値＝2.21）を利用して検定してみましょう