対応のないt検定（母分散が未知で等しい場合）

僕が作った架空のデータで練習しましょう。結果についてはご意見があると思いますが、統計学の練習のためのサンプルですのでご了承ください。

例題）回復期病棟で３週間入院した脳卒中患者を対象とした。X病院の患者群をX群、Y病院の患者群をY群としてFIM利得を比較した。両群の患者属性、入院時FIM、治療内容については傾向スコアにて調整した

データの準備と要約

library(tidyr)
library(ggplot2)

同じ分散をもつ正規分布から抽出したサンプル t-test を使用します

X <- round(rnorm(28, 25, 10),0)
Y <- round(rnorm(31, 30, 10),0)

乱数なので出るたびに数値は異なりますので注意してください．ここでは下記のcsvファイルを使用して学習します．

データセットt-testをdatに格納します（ファイルの読み込み）

data <- read.csv("t-test.csv", header=T, fileEncoding="Shift-JIS")
head(data)

それぞれの群のサンプルサイズが異なり、また独立した群の比較なので、縦のデータに変換しましょう（縦のデータと横のデータ）

data_long <- gather(data, key = "group", value = "data", na.rm = TRUE)
head(data_long)

# 箱ひげ図を描画
ggplot(data_long, aes(x = group, y = data)) +
  geom_boxplot() +
  theme_minimal()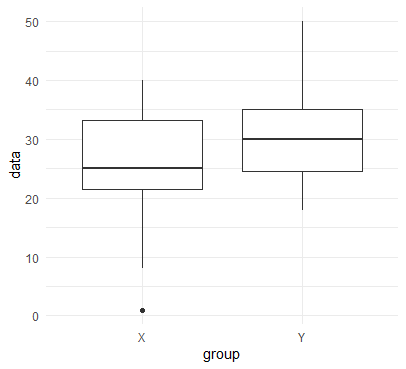

tidyr:: これはでパッケージtidyrを起動できます。つまり「::」を使用することで、library関数の記述は不要になります。

各グループの記述統計

psych::describeBy(data_long$data, data_long$group)

今回は同じ分散を設定した正規分布からの乱数ですので等分散を仮定（var.equal=TRUE）した検定となります

t.test(data~group, var.equal=TRUE, data=data_long)

A群平均は25.11、B群平均は30.71、p値は0.022（＜0.05）となりました．有意水準5％であれば有意な差と言えます．

必要なのが検定の結果だけであればここまででOKです。ここからは、もう少し詳しく見ていきましょう。