二元配置分散分析（繰り返し測定なし）

平方和の分解

一元配置分散分析と同様の方法で平方和を分解します（分かりやすくするために例題の数値を当てはめて記載します）

全体平方和\(\displaystyle= \sum_{i = 1}^{3} \sum_{j = 1}^{5} (y_{ij}-\bar{y})^2\)

要因Aの平方和\(\displaystyle= \sum_{i = 1}^{3} \sum_{j = 1}^{5} (\bar{y_{i\cdot}}-\bar{y})^2=5\sum_{i = 1}^{3} (\bar{y_{i\cdot}}-\bar{y})^2\)

自由度：３－１＝２

要因Bの平方和\(\displaystyle= \sum_{i = 1}^{3} \sum_{j = 1}^{5} (\bar{y_{\cdot j}}-\bar{y})^2=3\sum_{j = 1}^{5} (\bar{y_{\cdot j}}-\bar{y})^2\)

自由度：５－１＝４

残差平方和\(\displaystyle= \sum_{i = 1}^{3} \sum_{j = 1}^{5} (y_{ij}+\bar{y}-\bar{y_{i\cdot}}-\bar{y_{\cdot j}})^2\)

自由度：（３－１）×（５－１）＝８

全体平方和 = 要因Aの平方和 + 要因Bの平方和 + 残差平方和

➡証明

二元配置分散分析の統計モデルより

$y_{ij}=\mu + \alpha_{i} + \beta_{j} + e_{ij}$

$y_{ij}-\mu=\alpha_{i} + \beta_{j} + e_{ij}$

両辺の二乗和

$\sum\sum(y_{ij}-\mu)^2=\sum\sum(\alpha_{i} + \beta_{j} + e_{ij})^2$

偏差の和は0なので、 $\sum e_{ij}=0$、$\sum \sum \alpha_{i} \beta_{j}=0$

以上のことから

$\sum\sum(y_{ij}-\mu)^2= \sum(\alpha_{i})^2 + \sum(\beta_{j})^2 + \sum\sum(e_{ij})^2$

ゆえに、全体平方和 = 要因Aの平方和 + 要因Bの平方和 + 残差平方和

詳細は下記のページをご参照ください

一元配置分散分析

リハビリテーション統計学で利用頻度の高い分散分析の基礎となります。歩行が自立している高齢者のバランストレーニングの効果を確認するために、床反力計を使用して足圧中心(COP)の総軌跡長を30秒間評価した。年齢別に差があるか有意水準5％で検定してみましょう。

y2pt.com

2023.01.16

検定

平均平方和

勉強のために要因Bの平均平方和も求めてみましょう

再掲

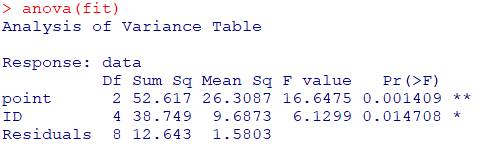
分散分析表の値を確認してみましょう

#全体の平均
ybar <- mean(dat2$data)

#A群平方和
(Agun <- sum(
    (mean(dat2[dat2$point=="PT1w", "data"]) - ybar)^2*5 +
    (mean(dat2[dat2$point=="PT2w", "data"]) - ybar)^2*5 +
    (mean(dat2[dat2$point=="PT3w", "data"]) - ybar)^2*5
))

#B群平方和（同じ計算の繰り返しはfor関数が便利です）
vec1 <- c()
vec2 <- c()
for(a in c("A","B","C","D","E")){
    p <- (mean(dat2[dat2$ID==a, "data"]) - ybar)^2*3
    vec1 <- c(p)
    vec2 <- c(vec2, vec1)
}
(Bgun <- sum(vec2))

#残差平方和=全体平方和ーA群平方和ーB群平方和 
(Zan <- sum((dat2$data - ybar)^2) -
    Agun -
    Bgun
)

Rの答えと同じになりました

F値

あとは簡単です

平均平方和＝平方和÷自由度

F値＝群平均平方和÷残差平均平方和

要因AのF値\(=\dfrac{Agun/2}{Zan/8}\)

要因BのF値\(=\dfrac{Bgun/4}{Zan/8}\)

#要因AのF値
(Fa <- (Agun/2)/(Zan/8))
#要因BのF値
(Fb <- (Bgun/4)/(Zan/8))

F検定

要因A（PT週）の効果

自由度(2, 8)のF分布で検定します

pf(Fa, 2, 8, lower.tail=F)

F分布

血圧測定した結果、A群50名の分散10mmHg, B群30名の分散5mmHgであった。A群とB群の母分散は等しいと言えるか？F分布はリハビリテーション統計学の検定で頻出する確率分布です。

y2pt.com

2023.01.01