二元配置分散分析（繰り返し測定あり）

平方和の分解

\(\sum\sum\sum(y_{ijk}-\bar{y})^2 = \)

\(\quad \sum\sum\sum(\bar{y_i..}-\bar{y})^2+ \)

\(\quad \sum\sum\sum(\bar{y_{.j.}}-\bar{y})^2+\)

\(\quad \sum\sum\sum(\bar{y_{ij.}}-\bar{y_{i..}}-\bar{y_{.j.}}+\bar{y})^2+\)

\(\quad \sum\sum\sum(y_{ijk}-\bar{y_{ij.}})^2\)

便宜上、上記の偏差平方和を以下のような名称にします

総平方和＝要因A平方和＋要因B平方和＋交互作用平方和＋残差平方和

例題では各グループのサンプルサイズが同じなので以下のように書けます

\(\sum\sum\sum(y_{ijk}-\bar{y})^2 = \)

\(\quad 10*\sum\sum(\bar{y_i..}-\bar{y})^2+ \)

\(\quad 15*\sum\sum(\bar{y_{.j.}}-\bar{y})^2+\)

\(\quad 5*\sum\sum(\bar{y_{ij.}}-\bar{y_{i..}}-\bar{y_{.j.}}+\bar{y})^2+\)

\(\quad \sum\sum\sum(y_{ijk}-\bar{y_{ij.}})^2\)

これで分散分析表ができます

分散分析表

再掲

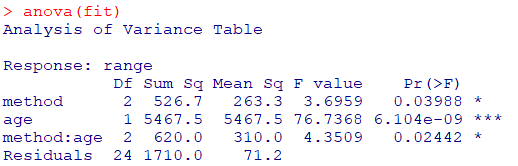
3つの帰無仮説が全て棄却されました

Rの結果を確認してみましょう

m <- mean(dat3$range)

#要因A平方和
10*(149.5-m)^2 +
10*(142.5-m)^2 +
10*(152.5-m)^2 

#要因B平方和
15*(161.67-m)^2 +
15*(134.67-m)^2

#交互作用平方和
5*(162-149.5-161.67+m)^2 +
5*(137-149.5-134.67+m)^2 +
5*(162-142.5-161.67+m)^2 +
5*(123-142.5-134.67+m)^2 +
5*(161-152.5-161.67+m)^2 +
5*(144-152.5-134.67+m)^2

#残差平方和
sum(
(dat3[dat3$age=="age60" & dat3$method=="A", "range"]-162)^2 +
(dat3[dat3$age=="age60" & dat3$method=="B", "range"]-162)^2 +
(dat3[dat3$age=="age60" & dat3$method=="AB", "range"]-161)^2 +
(dat3[dat3$age=="age80" & dat3$method=="A", "range"]-137)^2 +
(dat3[dat3$age=="age80" & dat3$method=="B", "range"]-123)^2 +
(dat3[dat3$age=="age80" & dat3$method=="AB", "range"]-144)^2 
)
#もっとスマートな方法がみつかったら更新します