級内相関係数, Case1, ICC(1, 1), ICC(1, k)

ICC(1, 1)の考え方
ICC(1, k)　k回の計測結果の平均値が対象

ICC(1, 1)の考え方

評価者の誤差(test1, test2, test3)が小さい場合、全体の分散には真の分散が影響しいてる

$\sigma^2_T$：真の分散（真の検査結果のバラツキ）

$\sigma^2_W$：誤差による分散

したがって

$ICC(1,1)$

$=\dfrac{真の分散}{真の分散 + 誤差による分散}$

$=\dfrac{\sigma^2_T}{\sigma^2_T+\sigma^2_W}$

ICC(1,1) が１に近いと３回測定した誤差の影響が小さく、「３回測定した結果の信頼性が高い」と結論付けます

統計モデル

${y_{ij} = \mu+\alpha_i+e_{ij}}$

$i=1, \dots , n \quad j=1, \dots ,k $

$\alpha_i \sim N(0, \sigma_T^2) \quad e_{ij} \sim N(0, \sigma_W^2)$

平均平方和よりICCを求める

$\sum\sum(y_{ij}-\bar{y})^2 = \sum\sum(\bar{y_i}-\bar{y})^2 + \sum\sum(y_{ij}-\bar{y_i})^2$

（詳細は一元配置分散分析をご参照ください）

ここでは

総平方和＝患者平方和＋残差平方和

とします

言葉を定義します。
患者平均平方和の期待値
BMS（between-targets mean square）
残差平均平方和の期待値
WMS（whitin-target mean square）
原文通りに群間と群内という言葉で訳されていることが多いようです。ここでは理解しやすいように患者と残差とします。各患者の真の測定値が全体の分散に影響する効果、残りの誤差が全体の分散に影響する効果という意味です。

$BMS = 3*\sigma^2_T+\sigma^2_W$

$WMS = \sigma^2_W$

ここがICCで一番重要なところですが、あまりに唐突なので最下段で証明します

$ICC(1,1)$

$=\dfrac{\sigma^2_T}{\sigma^2_T+\sigma^2_W}$

$=\dfrac{BMS-WMS}{BMS+(3-1)WMS}$

分散分析表

分散分析表からBMSとWMSを当てはめてICC(1, 1)を算出してみましょう

fit <- lm(data ~ ID, data=dat2)
anova(fit)

Analysis of Variance Table

Response: data
          Df Sum Sq Mean Sq F value    Pr(>F)    
ID         9  22163  2462.5  50.153 9.014e-12 ***
Residuals 20    982    49.1

平均平方和からICCを算出します

#ICC(1,1) 
BMS <- 2462.5
WMS <- 49.1
(BMS-WMS)/(BMS+(3-1)*WMS)

> (BMS-WMS)/(BMS+(3-1)*WMS)
[1] 0.9424767

答えは合っています

ICC(1,1)≒0.942

ICC(1,1) の95％信頼区間

Rの関数で求めた95％信頼区間をF分布を使用した分散比の信頼区間から求めてみます

$ICC(1,1) = \dfrac{BMS-WMS}{BMS+(3-1)WMS} = \dfrac{\dfrac{BMS}{WMS}-1}{\dfrac{BMS}{WMS}+(3-1)}$

分散比（$\dfrac{BMS}{WMS}$）の95%信頼区間を代入して、ICC(1,1)の信頼区間を求めます

$\dfrac{BMS}{F_{0.975}(9, 20)*WMS} \quad ～ \quad \dfrac{BMS}{F_{0.025}(9, 20)*WMS}$

BMS <- 2462.5
WMS <- 49.1

#F値
(f1 <- qf(0.025, 9, 20))
(f2 <- qf(0.975, 9, 20))
 
#分散比の信頼区間
(v1 <- BMS/(WMS*f2))#下限はf2を使用
(v2 <- BMS/(WMS*f1))#上限はf1を使用

#ICCの信頼区間
(v1-1)/(v1+3-1)#下限
(v2-1)/(v2+3-1)#上限

> #F値
> (f1 <- qf(0.025, 9, 20))
[1] 0.2727095
> (f2 <- qf(0.975, 9, 20))
[1] 2.836546
>  
> #分散比の信頼区間
> (v1 <- BMS/(WMS*f2))#下限はf2を使用
[1] 17.68092
> (v2 <- BMS/(WMS*f1))#上限はf1を使用
[1] 183.9054
> 
> #ICCの信頼区間
> (v1-1)/(v1+3-1)#下限
[1] 0.8475681
> (v2-1)/(v2+3-1)#上限
[1] 0.9838628

詳しくはF分布(分散比の95%信頼区間)をご参照ください

ICC(1, k)　k回の計測結果の平均値が対象

$k=$3 回計測した平均値を算出

(m <- aggregate(
    data ~ ID,
    data=dat2,
    FUN=mean
))

   ID     data
1   1 15.33333
2   2 27.33333
3   3 37.33333
4   4 43.33333
5   5 50.33333
6   6 70.00000
7   7 78.66667
8   8 87.33333
9   9 94.33333
10 10 92.66667

グラフにしてみましょう

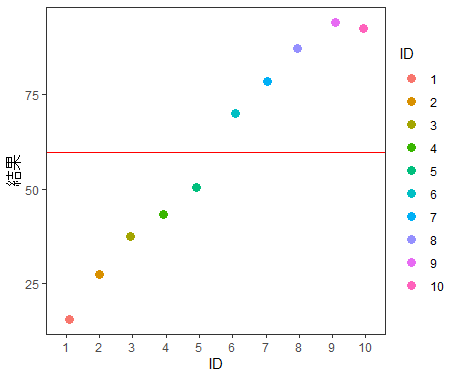
#グラフの描き方
g1 <- ggplot2::ggplot(
    m,
    aes(x = ID, y = data)
)

g2 <- g1 + geom_jitter(
    height=0, width =0.1, size = 3,
    aes(colour = ID)
) 

g2 + theme_test() + xlab("ID") +ylab("結果") +
    geom_hline(
        aes(yintercept = mean(dat2$data)),
        color = "red"
  )