irisを使用した単回帰分析
まずは最小二乗法
R
dat = iris
fit1 <- lm(Sepal.Length ~ Sepal.Width, data = dat)
summary(fit1)
残差の標準誤差や決定係数などが算出されます。
またF値やp値は次に示すような分散分析の結果になります。
R
anova(fit1)
次に最尤推定法による単回帰分析(lmがglmに変わるだけ・・・です)
もちろん答えは同じです
R
fit2 <- glm(Sepal.Length ~ Sepal.Width, data = dat)
summary(fit2)
ただし対数尤度を利用した解析結果ですのでdeviance、AICが算出されます
確率分布は正規分布で、リンク関数は恒等リンクがデフォルトなので、本当は以下のように書かれています(算出結果は全く同じ)
R
fit3 <- glm(Sepal.Length ~ Sepal.Width, family = gaussian (link = identity), data = dat)
summary(fit3)
family = gaussianのリンク関数は、 identity, log, inverseが使用できるようです
The gaussian family accepts the links (as names) identity, log and inverse
ちなみにリンク関数を変えたら、(当たり前ですが)異なる結果となります
R
fit4 <- glm(Sepal.Length ~ Sepal.Width, family = gaussian(link=log), data = dat)
summary(fit4)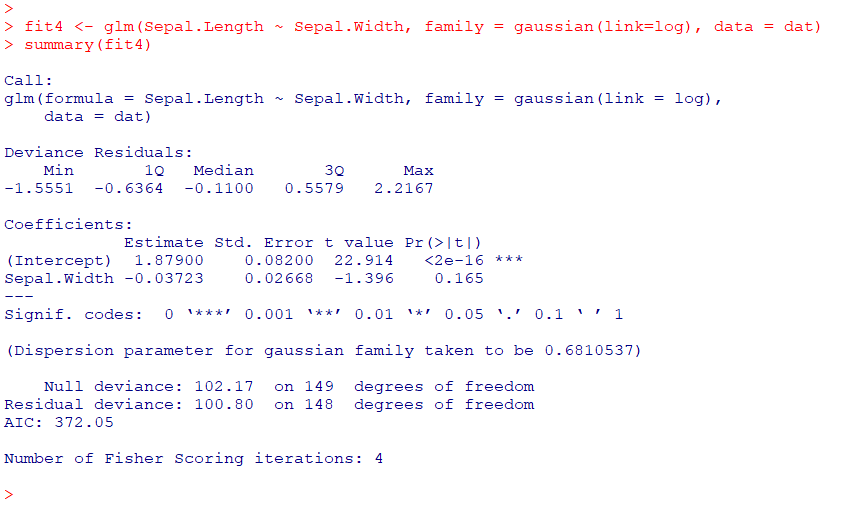




コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください