ロジスティック回帰 (1)

モデルの適合度判定

対数尤度：$l_{\theta}=\sum(y_i(\beta_0+\beta_1x_i)-n_ilog(1+e^{\beta_0+\beta_1x_i}))$

逸脱度（deviance）：$deviance = -2 \, × $ 対数尤度

対数尤度から求める逸脱度（deviance）は、モデルの当てはまりの「悪さ」を意味しています。Rは各モデルのdevianceの差を算出します。最も当てはまりのよいFull modelと最も当てはまりの悪いNull modelとの差をNull deviance、回帰分析モデルとフルモデルとの差をResidual devianceといいます。

最大逸脱度（$D_{max}$）= Null modelの逸脱度 (Null devianceではありません)

➡　Null model : 説明変数のないモデル＝切片モデル：最も当てはまりの悪いモデル

最小逸脱度（$D_{min}$）= Full modelの逸脱度

➡　Full model：全てのデータを二項分布に当てはめたモデル

Rでは Null deviance と Residual deviance が算出されます

Null model

#Null modelでのロジスティック回帰
null <- glm(
    cbind(満足, 患者数-満足)  ~ 1,
    family = binomial,
    data = dat
) 
print(null)

回帰分析によるモデル

再掲

fit <- glm(
    cbind(満足, 患者数-満足) ~ 単位数, 
    family=binomial, 
    data=dat
)
summary(fit)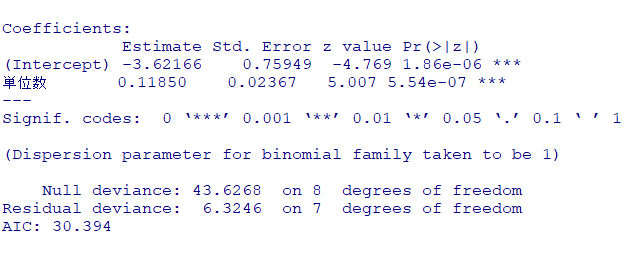

Deviance(逸脱度)の求め方

RのlogLik関数で各モデルによる最大対数尤度が算出されます（便利ですね・・・）

#最大逸脱度（Null modelの逸脱度）
-2*logLik(null)

#回帰分析モデルの逸脱度
-2*logLik(fit)

#最小逸脱度（Full modelの逸脱度）
-2*sum(log(dbinom(dat$満足, dat$患者数, dat$満足/dat$患者数)))

★最小逸脱度（Full modelの逸脱度）の求め方

Full modelの対数尤度：$lmin=\log(\sum (P_i^{y_i}(1-P_i)^{n_i-y_i})))$

$\beta_0, \beta_1$ を推定するのではなく、$P_i$には実測値から得らた確率 ($\dfrac{満足}{患者数}$) を直接挿入します

最小逸脱度$=-2*lmin$

尤度比検定（ｶｲ二乗検定による方法）

Null modelと回帰分析モデルの最大対数尤度の差に-2を掛けた値がｶｲ二乗分布に近似することを利用した検定

帰無仮説：Null model

対立仮説：回帰分析によるモデル

尤度比検定の統計量

-2*(logLik(null) - logLik(fit))

P値

pchisq(-2*(logLik(null) - logLik(fit)), 1, lower.tail=F)

下記のように分散分析からも求めることができます

anova(null, fit, test = "Chisq")

Model1 : Null model
Model2 : 回帰分析によるモデル

検定結果は、p<0.001となり回帰分析モデルが真のモデルであるという結果になりました

帰無仮説は棄却され対立仮説の回帰モデルによる推定が支持されることになります

★サンプルサイズが小さい場合には、パラメトリックブートストラップ法により求めます（参考文献にはサンプルサイズが100くらいであればｶｲ二乗分布近位は正確なP値が得られないと書かれています）

参考文献：久保拓弥. (2012). データ解析のための統計モデリング入門 (Vol. 267). 岩波書店.