ログランク検定（log-rank test）

2群の生存率曲線に有意な差があるか・・・を検定する方法を紹介します。ログランク検定は、2群の生存時間データを比較するために使用されるノンパラメトリック検定です。以下のページに掲載されているデータを使用させていただきました。いつも大変お世話になっております。

統計学入門−第11章 (snap-tck.com)

データの準備と要約
カプランマイヤー曲線（Kaplan-Meier曲線）
Rでログランク検定（log-rank test）
ログランク検定の検定統計量
- ログランク検定の統計量
参考）重み付けした統計量

データの準備と要約

必要なパッケージをダウンロードしておきます（ダウンロード方法について）

library(survival)
library(survminer)

サンプルを準備します（Rにcsvファイルを読み込む）

surv サンプルのダウンロード

dat <- read.csv("surv.csv", header=T, fileEncoding = "Shift-JIS")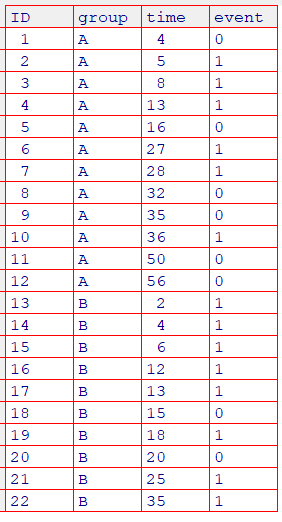

group列: A群＝12名、B群＝10名
time列: 時期
event列: イベント発生（1: 死亡, 0: 脱落、打ち切り）

カプランマイヤー曲線（Kaplan-Meier曲線）

時期とイベントのデータセット

time_event <- Surv(time = dat$time, event = dat$event)
print(time_event )

数値は時期、＋は「打ち切り」あり

fit <- survfit(time_event ~ group, data=dat)
summary(fit)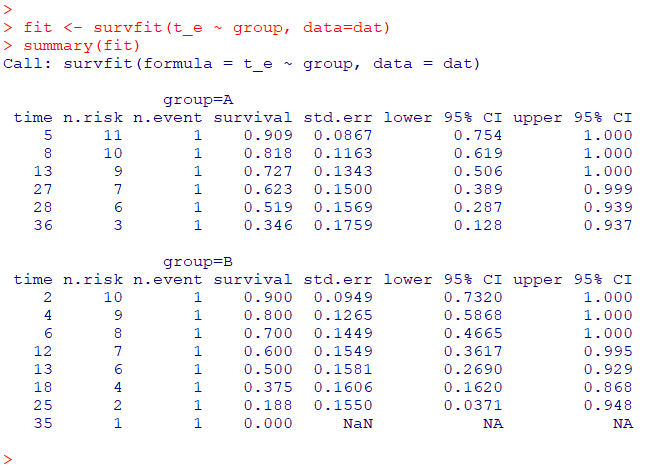

# カプランマイヤー曲線
g1 <- ggsurvplot(
  fit, data = dat, pval = TRUE,
  risk.table = TRUE, #各時期のリスク集合の数
  break.time.by = 6) #ｘ軸の間隔
print(g1)

p値はログランク検定の結果

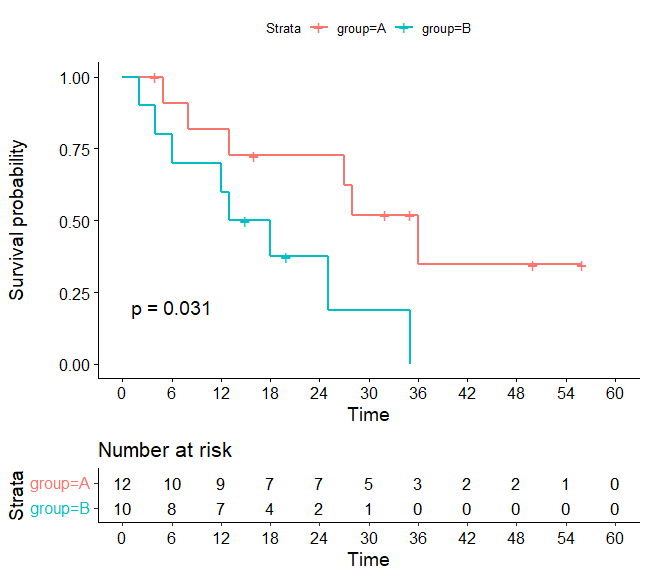
Rでログランク検定（log-rank test）

# ログランク検定の実行
logrank <- survdiff(time_event ~ group, data = dat)
# 検定結果の表示
print(logrank)

p値＝0.03となり、有意差が認められました。検定の結果のみでよろしければ、ここまででOKです。ここからは、もう少し詳しく見ていきます。

ログランク検定の検定統計量

時間でソートしたデータ

dat_sorted <- dat[order(dat$time), ]
#View(dat_sorted )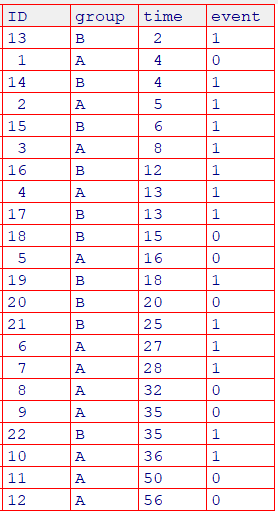

（event; 1=死亡、0=脱落、打ち切り）

超幾何分布より期待値と分散を求めます

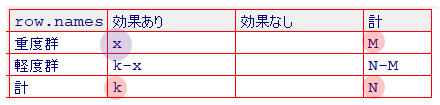
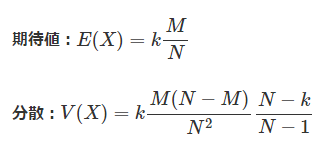
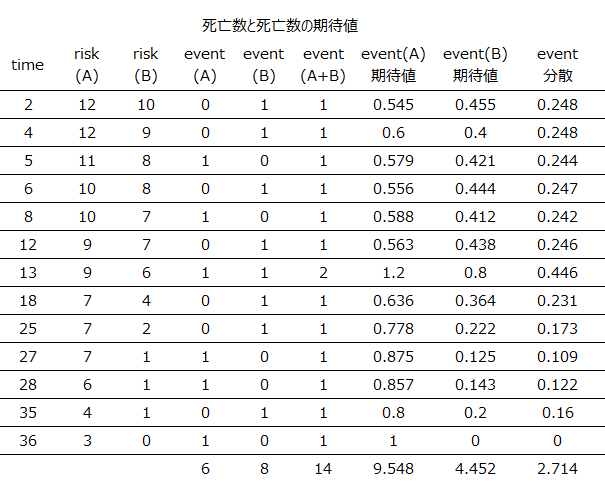
期待値と分散の一覧は以下のようになります（event: 1＝死亡、0＝脱落、打ち切り）

この一覧を使用して、各検定の統計量が計算されます

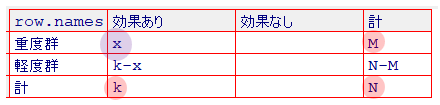
M = risk(A)
N = risk(A) + risk(B)
X = event(A)
k = event(A+B)

Mantel-Haenszel統計量

一般的にログランク検定し使用されている統計量

ログランク検定の検定統計量は、比較されるグループが2つの場合、自由度1のカイ二乗分布に従います

イベント（ここでは「死亡」）が発生する時点で2×2の分割表を作成し、カイ二乗統計量からP値を算出します

各時間での死亡数、期待値、分散から有意な差があるかどうかを判断します

logrank <- survdiff(Surv(time, event) ~ group, data = dat)
print(logrank)

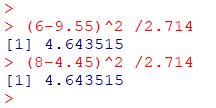
Mantel-Haenszel統計量 = 4.64（自由度1のカイ二乗分布に従う）

期待値と分散の一覧表よりMantel-Haenszel統計量を求める方法

$w_j＝1$で重み付けしたカイ二乗統計量

$\chi^2(Mantel-Haenszel) = \dfrac{(\sum(d_{1j}-e_{1j}))^2}{\sum{v_i}}$

(6-9.55)^2 /2.714
(8-4.45)^2 /2.714

（A群もB群も同じ解になります）

ログランク検定の統計量

Mantel-Haenszel統計量とは異なる方法でカイ二乗統計量を算出する方法

ログランク統計量($\chi_{LR}^2$)＝1.32 + 2.83 = 4.15（自由度1のカイ二乗分布に従う）

期待値と分散の一覧表よりログランク統計量を求める方法

$d_{Ai}$: group A の死亡数
$e_{Ai}$: group A の死亡数を確率変数とした場合の期待値（超幾何分布）
$d_{Bj}$: group B の死亡数
$e_{Bj}$: group B の死亡数を確率変数とした場合の期待値（超幾何分布）

$\chi_{LR}^2=\dfrac{(\sum(d_{Ai}) – \sum(e_{Ai}))^2}{\sum(e_{Ai})}+\dfrac{(\sum(d_{Bj}) – \sum(e_{Bj}))^2}{\sum(e_{Bj})}$

(6-9.548)^2/9.548 + (8-4.452)^2/4.452

参考）重み付けした統計量

混乱しますが、以下のような統計量もあります（他にもあります）

$w_k$で重み付けしたカイ二乗統計量

$\chi^2_{w_k} = \dfrac{(\sum{w_k}(d_{1k}-e_{1k}))^2}{\sum{w_k^2}v_k}$

$d_{1k} : $ イベント数
$e_{1k} : $ イベント期待値
$v_k : $ イベント分散

Rを使用したｐ値の求め方（参考ページ）

#ログランク検定（method = "1"）
surv_pvalue(fit, data = dat, method = "survdiff")
#Gehan-Breslow
surv_pvalue(fit, data = dat, method = "n")
#Tarone-Ware
surv_pvalue(fit, data = dat, method = "sqrtN")

method =

“1“または”survdiff” : 通常のログランク検定（Mantel-Haenszel統計量）、遅い時期の差異を検出するのに敏感
“n“：Gehan-Breslow（一般化ウィルコクソン）, $w_k＝N$ で重み付け, 早期の差異を検出
“sqrtN“：Tarone-Ware , $w_k＝\sqrt{N}$ で重み付け, 早期の差異を検出

詳細については下記論文をご参照ください

Gehan A. A Generalized Wilcoxon Test for Comparing Arbitrarily Singly-Censored Samples. Biometrika 1965 Jun. 52(1/2):203-23.
Tarone RE, Ware J 1977 On Distribution-Free Tests for Equality of Survival Distributions. Biometrika;64(1):156-60.
Peto R, Peto J 1972 Asymptotically Efficient Rank Invariant Test Procedures. J Royal Statistical Society 135(2):186-207.
Fleming TR, Harrington DP, O’Sullivan M 1987 Supremum Versions of the Log-Rank and Generalized Wilcoxon Statistics. J American Statistical Association 82(397):312-20.