t分布 | 統計学備忘録リハビリテーション統計学

ｔ統計量
確率密度関数
t分布のグラフ

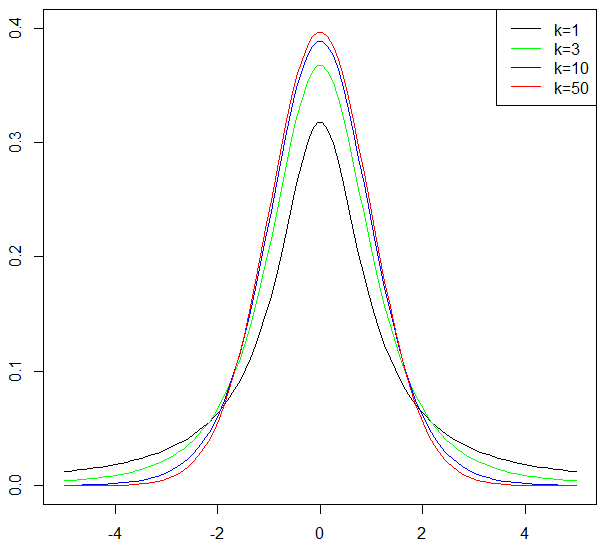
ｔ統計量

$\bar{X}$ : 標本の平均（いわゆるデータの平均値）

$μ$ : 母集団の平均値（検定で推定したい値）

$σ^{2}$ : 母集団の分散（この母分散が未知）

母分散が既知の場合の統計量

$Z = \frac{\bar{X} - μ}{\sqrt{\frac{σ^{2}}{n}}} \sim N (0, 1)$

しかし $σ^{2}$ が不明なので、この統計量は使用することができません

そこで $σ^{2}$ の代わりに標本不偏分散 $s^{2}$ を使います

標本不偏分散: $s^{2} = \frac{1}{n - 1} Σ (x_{k} - \bar{X})^{2}$ $(k = 1, 2, \dots, n)$

母分散が未知の場合、統計量はこの標本不偏分散を使用したｔ統計量となります

ｔ統計量の分布は標準正規分布とカイ二乗分布の比になっています

証明

t統計量: $t = \frac{\bar{X} - μ}{\sqrt{\frac{s^{2}}{n}}} = \frac{\bar{X} - μ}{\sqrt{\frac{σ^{2}}{n}} \sqrt{\frac{s^{2}}{σ^{2}}}} = \frac{\frac{\bar{X} - μ}{\sqrt{\frac{σ^{2}}{n}}}}{\sqrt{\frac{\frac{(n - 1) s^{2}}{σ^{2}}}{n - 1}}}$

$\frac{\bar{X} - μ}{\sqrt{\frac{s^{2}}{n}}} \sim N (0, 1)$

$\frac{(n - 1) s^{2}}{σ^{2}} \sim χ^{2} (n - 1)$ 　自由度( $n - 1$ )の $χ^{2}$ 分布

証明終わり

よって、統計量tが従う分布を自由度( $n - 1$ )のt分布といいます

$t = \frac{\bar{X} - μ}{\sqrt{\frac{s^{2}}{n}}}$

studentのt分布という名前でも知られています。この分布を定義したのはWilliam Gossetです。ギネスビール社に勤めていた彼は、会社に内緒でこのｔ分布に関する論文（1908）を投稿するためにStudentというペンネームを使ったということです。

確率密度関数

上記の証明よりZとWが独立かつ $Z \sim N (0, 1), W \sim χ^{2} (k)$ を満たす場合

$\frac{Z}{\sqrt{\frac{W}{k}}}$ が従う分布を自由度kのｔ分布といい、 $t (k)$ と標記します

確率密度関数： $f (x; k) = \frac{1}{\sqrt{k} B (\frac{k}{2}, \frac{1}{2})} (1 + \frac{x^{2}}{k})^{- \frac{k + 1}{2}}$

ベータ関数 $B (α, β) = \int_{0}^{1} x^{α - 1} (1 - x)^{β - 1} d x$

期待値： $0 (k > 1)$

分散： $\frac{k}{k - 2} (k > 2)$

自由度15のt分布でX＝3のときの確率を求めてみましょう

例） $d f = 15, x = 3$

$B (\frac{15}{2}, \frac{1}{2}) = \int_{0}^{1} x^{7.5 - 1} (1 - x)^{0.5 - 1} d x = 0.6580778$

f <- function(x) (x^(7.5-1))*(1-x)^(0.5-1)
(i <- integrate(f, 0, 1))
(t <- (1/(sqrt(15)*0.6580778 ))*((1+(3^2/15))^(-8)))

Rの関数から求めてみましょう

dt(x=3, df=15)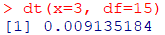

t分布のグラフ

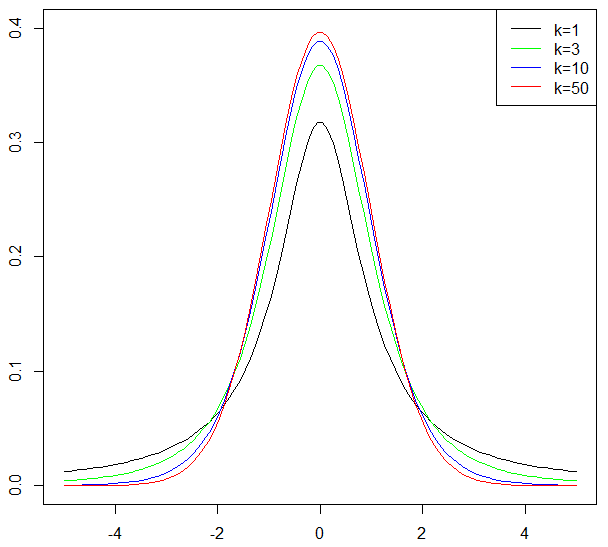
#グラフ
x <- seq(-5, 5, length=100)
data <- data.frame(
    t1=c(dt(x, 1)),
    t3=c(dt(x, 3)),
    t10=c(dt(x, 10)),
    t50=c(dt(x, 50))
)
 
cols <- c("black", "green", "blue", "red")
ltys <- c(rep(1, 4))
 
plot(
    0, 0, type = "n",
    xlim=c(-5, 5), ylim=c(0, 0.4),
    xlab="", ylab=""
)
 
for (i in 1:ncol(data)) {
    lines(
        x, data[, i], lty=ltys[i], col=cols[i]
    )
}

legend(
        "topright",
        legend=c("k=1", "k=3", "k=10", "k=50"),
        col=cols,
        lty="solid"
)

ｔ統計量

確率密度関数

t分布のグラフ

コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください

コメント欄『間違い』や『分かりにくい部分』などのご意見もお寄せください