データの準備と要約

ここでは方法のみを記載してます。例題は統計学の勉強のためのものですので、実際の解釈とは異なる部分もあるとおもいますが、ご了承ください。
使用するパッケージ
library(twang)
library(tidyverse)
library(Matching)
library(WeightIt)%>% 演算子を使うのでtidyverseを入れときましょう(magrittrやdplyrでも可)
Rのパッケージtwangに入っているデータセットlindnerを使用します
ファイルlinderをdatに読み込みます(ファイルの読み込み方)
datにlindnerを格納します
dat <- read.csv("lindner.csv", header=T, fileEncoding = "UTF-8")サンプルの確認
head(dat)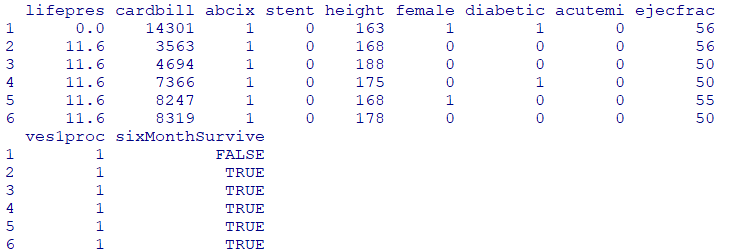
ヘルプでデータセットの詳細を調べます
??lindner経皮冠動脈インターベンション(PCI:Percutaneous Coronary Intervention )
996 人の患者で収集された 10 個の変数のデータ フレーム
cardbill: 患者の最初の PCI から 6 か月以内に発生した心臓関連の費用
abcix: 1=アブシキシマブ投与の有、0=通常のPCI治療
stent:1=冠動脈ステント展開あり
height:身長
female:性別(女性=1)
diabetic:1=糖尿病あり
acutemi:1=急性心筋梗塞
ejecfrac:左室駆出率
ves1proc:患者の最初の PCI 手順に関与した血管の数
sixMonthSurvive:TRUE=PCI後6ヶ月で生存
sixMonthSurviveを数字にしてきます(このサイトでは2値変数を0,1に変換することを基本にしてます)
#生存=1, 死亡=0
dat$suv <- as.integer(dat$sixMonthSurvive)アブシキシマブ投与の有無による死亡率の差を求めたい
基準の記載
dat$abcix <- as.factor(dat$abcix) %>%
relevel(, ref="1")
dat$suv <- as.factor(dat$suv) %>%
relevel( , ref="0")
tab <- table(dat[,c("abcix", "suv")]) %>%
print()Rは若い数字が基準になるのですがrelevel関数で基準を明確に定義しておくことをお勧めします

今度はfactorに変換しました。factorにはlevelが付与されるため、分割表の基準を設定できるからです。下記の分割表の基準はabcix=1、suv=0です(暴露あり&死亡)。
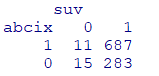
アブシキシマブ投与の有無による死亡率の差は約3.5%
#暴露群のリスク
(A <- 11/(11+687))
#非暴露群のリスク
(B <- 15/(15+283))
#暴露あり群の暴露なし群に対するリスク比
A/B
#リスク差(非暴露群のリスク-暴露群のリスク)
B-A
しかし、この死亡率の差には糖尿病の有無が関連していたとします
(実際の解析のときには、なんらかの根拠が必要です)
注意
パッケージEpiなどを使用する場合、基準が若い数字になります
つまり暴露なし&死亡が基準となります
library(Epi)
twoby2(tab)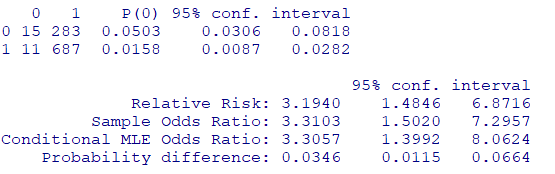
基準をそのまま使用する場合には、もとめた式をそのままtwoby2関数に渡します
twoby2(table(dat[,c("abcix", "suv")]))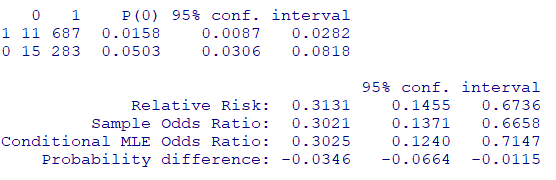
ロジスティック回帰分析
y=diabetic:暴露群(糖尿病あり)、非暴露群(糖尿病なし)
説明変数にabcix、diabetic、sixMonthSurvive以外の全変数を投入
fit <- glm(
diabetic ~ stent + height + female + acutemi + ejecfrac + ves1proc ,
family = binomial(link = "logit"),
data = dat
)
summary(fit)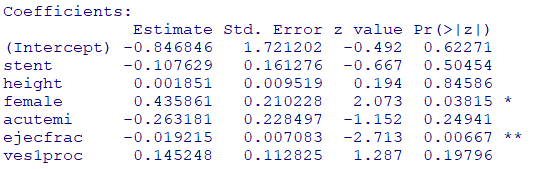
ステップワイズで変数選択(少々乱暴ですが・・・)
step(fit)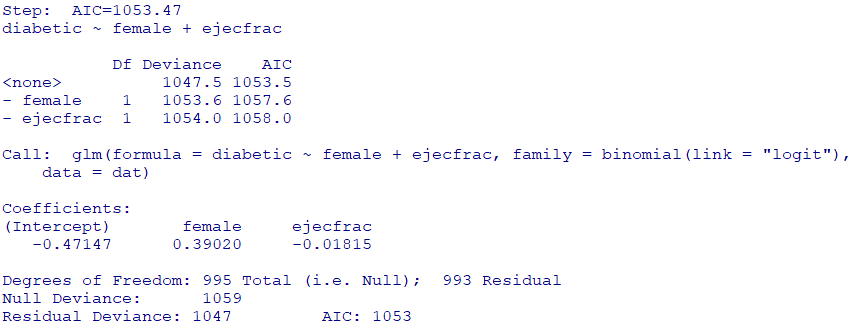
残った変数のみで、再度ロジスティック回帰を実行して傾向スコアを求めます
fit2 <- glm(
diabetic ~ female + ejecfrac,
family = binomial(link = "logit"),
data = dat
)
summary(fit2)
傾向スコア(最初の10人分のスコアを表示)
ps <- fit2$fitted.values
ps[1:10]
この傾向スコアをもとにマッチングします
attach(dat)
psm <- Matching::Match(
Y = as.integer(dat$suv) ,
Tr = (dat$abcix==1),
X = ps,
M=1,
caliper =0.3,
ties=FALSE,
replace = FALSE
)
detach(dat)
summary(psm)Y=傾向スコア調整後に比較したい値
Tr=比較対象(アブシキシマブ投与の有りと無しでマッチング)
X=傾向スコア
Z=バイアス調整を行いたい共変量を含む行列
M=検索して一致させるスカラー数。 デフォルトは 1 対 1 のマッチングとなっている。1対複数の設定が可能。
caliper=マッチング時に使用するキャリパー。 キャリパーとは、マッチングが許容される距離です。 キャリパーより大きい差のあるマッチングは除外されます。 キャリパーが指定されている場合、すべての共変量に使用されます。ベクトルが指定されている場合、X の各共変量にキャリパー値を指定する必要があります。キャリパーは標準化された単位です。 たとえば、キャリパー = .25 は、X の各共変量の .25 標準偏差と等しくないか、その範囲内にないすべての一致が除外されることを意味します。 一般に、観測値を削除すると、推定される量が変わることに注意してください。
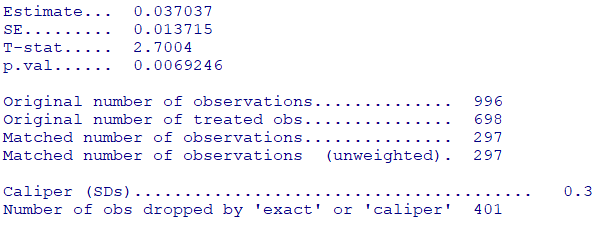
Original number of observations:被験者の総数
Original number of treated obs:糖尿病有りの総数
Matched number of observations:マッチングした総数
傾向スコアマッチング後の暴露有無による死亡率の差
#暴露群 abcix=1
treat <-dat[psm$index.treated,]
#非暴露群 abcix=0
control <-dat[psm$index.control,]
dat2 <-rbind(treat,control)
table(dat2[,c("abcix", "suv")])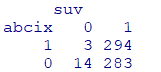
暴露の有無による死亡率の差は約2.5%
$\dfrac{427}{9+427}-\dfrac{149}{7+149}=0.02422959$
#暴露群のリスク
(A <- 3/(3+294))
#非暴露群のリスク
(B <- 14/(14+283))
#暴露あり群の暴露なし群に対するリスク比
A/B
#リスク差(非暴露群のリスク-暴露群のリスク)
B-A
IPTW(Inverse Probability of Treatment Weight)
(逆確率重み付け、逆数重み付け)
暴露群の重み:$重み=\dfrac{1}{傾向スコア}$
非暴露群の重み:$重み=\dfrac{1}{1-傾向スコア}$
IPTW <- WeightIt::weightit(
diabetic ~ female + ejecfrac,
data = dat,
method = "ps", #ロジスティック回帰によって傾向スコア
estimand = "ATE" #IPTW
)datに”傾向スコア”と”重み”を追加します
dat_IPTW <- mutate(
dat,
ps = IPTW$ps,
weight = IPTW$weights
)
head(dat_IPTW)SMRW(Standardized Mortality Ratio Weight)
暴露群:重み=1(そのままのデータを使用)
非暴露群:$重み=\dfrac{傾向スコア}{1-傾向スコア}$
SMRW <- WeightIt::weightit(
diabetic ~ female + ejecfrac,
data = dat,
method = "ps", #ロジスティック回帰によって傾向スコア
estimand = "ATT" #SMRW
)
dat_SMRW <- mutate(
dat,
ps = SMRW$ps,
weight = SMRW$weights
)
head(dat_SMRW)佐藤俊哉, & 松山裕. (2011). 交絡という不思議な現象と交絡を取りのぞく解析—標準化と周辺構造モデル—. 計量生物学, 32(Special_Issue), S35-S49.


