クロスオーバー試験（混合効果モデル）

1ページ　 2ページ　 3ページ

効果の検証

効果の検証

持ち越し効果（carry-over effect）がある場合

washout期間は十分に確保できていたか？

＊後発医薬品の生物学的同等性試験ガイドラインでは、washout期間 (休薬期間) が設定されています。

持ち越し効果の検定

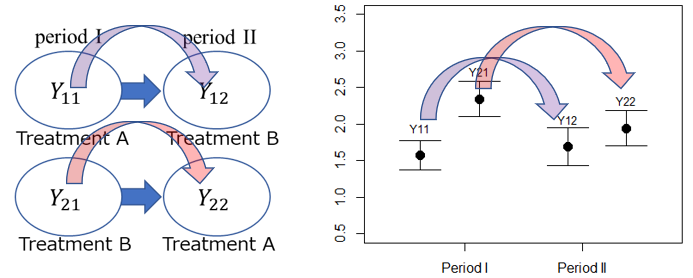
I期(治療A＋治療B)とII期(治療A＋治療B)の平均値の差の検定（対応のないt検定）により検証。検出力が低いので有意水準は10％が良い（折笠, 2016）。検定の結果 p<0.1 になった場合は、クロスオーバー試験は適用できません。

$\blacklozenge$ サンプルの持ち越し効果の検定

$Y_{11k}+Y_{12k}$ と $Y_{21k}+Y_{22k}$ の平均の差の検定

参考文献（折笠 2016）の図4の結果

# t test
t1 <- t.test(c(Y11 + Y12), c(Y21 + Y22) , var.equal=T)
print(t1)
# mean of AB－ mean of BA
mean(Y11 + Y12) - mean(Y21 + Y22)
# Standard error 
t1$stderr

p=0.1253（>0.1）のため持ち越し効果はないと判定します

治療効果（treatment effect）の検証　＜ｔ検定と混合効果モデル＞

対応のあるt検定

# Retrieve A and B data by ID (keeping sequence)
A_data <- data %>% filter(treatment == "A") %>% select(ID, sequence, point) %>% rename(point_A = point)
B_data <- data %>% filter(treatment == "B") %>% select(ID, sequence, point) %>% rename(point_B = point)

# Merge data using ID as the key
merged_data <- merge(A_data, B_data, by = "ID")

# Assign colors for s1 and s2
colors <- ifelse(merged_data$sequence.x == "s1", "blue", "red")

# Create the plot
par(mar = c(5, 4, 4, 6))  # Expand the right margin (for legend)
matplot(t(as.matrix(merged_data[, c("point_A", "point_B")])), type = "l", lty = 1, col = colors,
        xlab = "Treatment", ylab = "Point", xaxt = "n", main = "Comparison of Treatment A and Treatment B")

# Set x-axis labels
axis(1, at = c(1, 2), labels = c("A", "B"))

# Place the legend outside the plot
par(xpd = TRUE)  # Allow drawing outside the plot area
legend("topright", inset = c(-0.20, 0), legend = c("s1", "s2"), col = c("blue", "red"), lty = 1)#, title = "")
par(xpd = FALSE)  # Restore default drawing settings
par(mar = c(5.1, 4.1, 4.1, 2.1))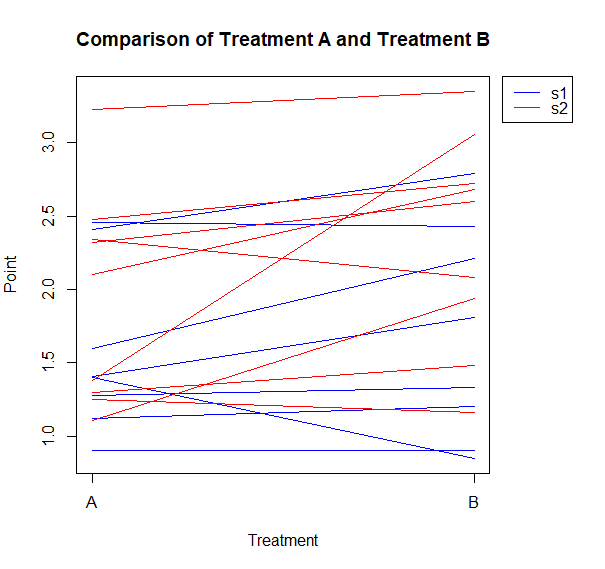

治療Aと治療Bの比較

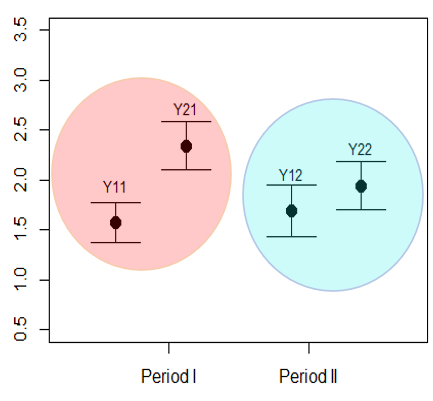
参考文献（折笠 2016）の図8の結果

# t test
t2 <- t.test(c(Y11, Y22) - c(Y12, Y21) )　
print(t2)
# Standard error 
t2$stderr

p=0.042なので治療Bが有意に高いことになります

混合効果モデルを用いることで、対応のある t 検定と同じ結果を得ることができます。本モデルはランダム切片モデルであり、各 ID ごとのランダム切片を線形回帰に取り入れています。これにより、ベースラインにおける個々の被験者の違い（ランダム効果）を調整しつつ、固定効果である treatment の影響を適切に分析できます。

t3 <- lmerTest::lmer(
    point ~  treatment + (1|ID),
    data = data
)
summary(t3)

A－B＝－0.2647, t値=－2.21, p値＝0.0421

(1|ID)によるランダム効果の組み込み
治療Aおよび治療Bにおいて、さらにPeriod IとIIを通じても、個人差が存在します。これらの個人差は(1|ID)を用いてランダム効果としてモデルに組み込むことができ、被験者ごとの反応の変動を効果的に捉えることが可能です。

ウィルコクソンの符号順位検定では以下のような結果となります (パッケージexactRankTestsを使用)

exactRankTests::wilcox.exact(
    c(Y11, Y22) , c(Y12, Y21), 
    paired=T, conf.int=T
)

検定統計量の結果が参考文献（折笠 2016）の図8の結果と異なります。詳細が分かれば追加で記載します。

混合効果モデル（対象者ID＝変量効果）

参考文献（折笠 2016）の図5の結果。
ランダム切片モデル（各 ID ごとのランダム切片を線形回帰に取り入れたモデル）。これにより、ベースラインにおける個々の被験者の違い（ランダム効果）を調整しつつ、固定効果である treatment 、period の影響を適切に分析できます。

fit1 <- lmerTest::lmer(
    point ~ treatment + period + (1|ID),
    data = data
)
summary(fit1)

period効果を考慮した場合の治療A－治療B平均値の推定値は－0.2565。p値＝0.0472なので治療Bが有意に高いことが分かります。

時期効果（period effect）の検証

参考文献（折笠 2016）の図6の結果。
period と treatment の位置を変えてますが、上述した混合効果モデルと同じです。

fit2 <- lmer(
    point ~ period + treatment + (1|ID),
    data = data
)
summary(fit2)

treatmentで調整したI期—II期の平均値の推定値は0.139。p=0.2595なので有意差は認められません。