ウェルチのt検定

2群の分散が等しくない場合のt検定は、ウェルチの検定（ウェルチのt検定、ウェルチの近似法）とも呼ばれています。

例題）回復期病棟で３週間入院した脳卒中患者を対象とした。A病院の患者群をA群、B病院の患者群をB群としてFIM利得を比較した。両群の患者属性、入院時FIM、治療内容については傾向スコアにて調整した。（分散が等しい例題と同じ内容ですが、サンプルが異なります）

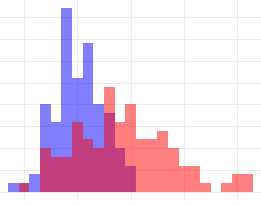
データの準備と要約

使用するパッケージ（パッケージのインストール）

library(psych)

同じ分散をもつ正規分布から抽出したサンプルを使用します（縦のデータセット）．データセットwelchをdatに格納します（ファイルの読み込み）．

dat <- read.csv("welch.csv", header=T, fileEncoding = "Shift-JIS")

サンプルwelchは下記の乱数から取り出した、母分散が異なる（A群25、B群400）独立した２群のセットです（実行するたびに数値は異なります）．

A <- round(rnorm(28, 25, 5),0)
B <- round(rnorm(31, 30, 20),0)

サンプル先頭6行を表示

head(dat)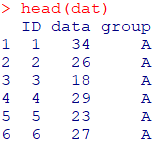

A群とB群の要約

#groupを名義変数に変更
dat$group <- factor(dat$group)

#各グループの要約
gsum <- psych::describeBy(dat$data, dat$group)
print(gsum)

箱ひげ図で確認します

boxplot(data~group, data=dat)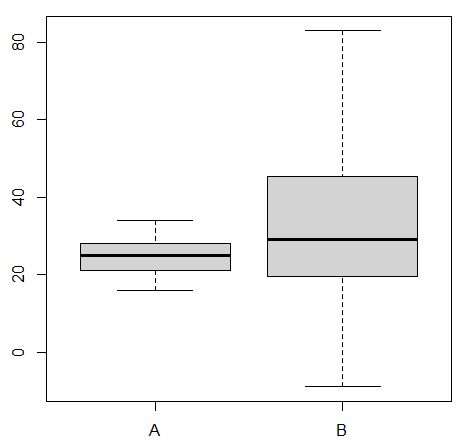

このように両群の分散の推定値の差が大きい場合、母分散のが等しいと想定することが難しくなります．このような場合にはWelchのt検定を実施します．

ウェルチのt検定

t.test(data~group, data=dat)

P=0.086となり有意差は認められませんでした

結果のみでよければ、ここまでです

ここからは、もう少し詳しく勉強してみましょう

等分散性の検定

両群の分散が等しいかどうかを検定（有意水準5％）します

帰無仮説：groupAの分散＝groupBの分散 ➡ 分散比＝$\dfrac{va}{vb}＝1$

分散比の分子と分母を確認します

str(dat$group)

分散比は $\dfrac{A}{B}$ となります

B群を分子に置く場合は以下のように書きます。

dat\$group <- relevel(dat\$group, ref=”B”)

この場合は分散比（F値）が異なる値になります。詳しくはF分布をご覧ください。

#等分散性の検定
var.test(data ~ group, data=dat)

F値とP値の求め方

#groupAの分散
va <- var(dat[dat$group=="A", "data"])
print(va)

#groupBの分散
vb <- var(dat[dat$group=="B", "data"])
print(vb)

分散比$=F=\dfrac{va}{vb}=\dfrac{21.59}{482.25}=0.045$

pf(va/vb, 28-1, 31-1)*2

帰無仮説は棄却され、A群とB群の分散は等しいとは言えない

本来であれば片側検定が妥当と思います。

参考ページ➡Fisherの正確検定

t値

分散が等しくない場合にはｔ値を次のように定義します

A群の平均＝\(\bar{A}\)
B群の平均＝\(\bar{B}\)
A群の母平均=\(\mu_a\)
B群の母平均=\(\mu_b\)
A群のサンプルサイズ=\(n_a\)
B群のサンプルサイズ=\(n_b\)
A群の不偏分散=\(s_a^2\)
B群の不偏分散=\(s_b^2\)

\(t=\dfrac{\bar{A}-\bar{B}}{\sqrt{\dfrac{s_a^2}{n_a}+\dfrac{s_b^2}{n_b}}}\)

このｔ値は近似的に自由度が次のようになるｔ分布に従うことが知られています

\(df=\dfrac{(\dfrac{s_a^2}{n_a}+\dfrac{s_b^2}{n_b})^2}{\dfrac{(\dfrac{s_a^2}{n_a})^2}{n_a-1}+\dfrac{(\dfrac{s_b^2}{n_b})^2}{n_b-1}}\)

t値と自由度

A群とB群の要約より

#サンプルサイズ
n1 <- gsum$A$n
n2 <- gsum$B$n

#不偏分散
v1 <- gsum$A$sd^2
v2 <- gsum$B$sd^2

#平均
mA <- gsum$A$mean
mB <- gsum$B$mean

#T統計量（T値）
(t <- (mA - mB)/sqrt(v1/n1 + v2/n2))

#自由度
(df <- ((v1/n1 + v2/n2)^2)/(((v1/n1)^2)/(n1-1) + ((v2/n2)^2)/(n2-1)))

Welchのt検定は、2つの母集団の平均が等しいかどうかを検定するために使用される統計手法です. この検定は、2つのサンプルが等しい分散を持たない場合やサンプルサイズが異なる場合にも適用できるように設計されています. しかし、Welchのt検定は、サンプルの分布が正規分布から大きく逸脱している場合、特に分布の歪度（skewness）が顕著な場合には、その結果が影響を受ける可能性があると言われています.