重回帰分析

回帰分析表と分散分析表
- 回帰分析表
- 分散分析表

回帰分析表と分散分析表

回帰分析表

#再掲
fit <- lm(
    FIM差 ~ BMI + 前FIMm + PT時間 , 
    data=dat
)
summary(fit)

今度は決定係数やF値が見えるところまでペーストしておきます

信頼区間と予測区間

導出は後日アップします！今回は方法のみ書いておきます。

#係数の信頼区間
confint ( fit , level = 0.95 )

#予測値の信頼区間
con <- predict(fit, newdata = dat, interval = 'confidence', level = 0.95)
head(con)

#予測値の予測区間
pre <- predict(fit, newdata = dat, interval = 'prediction', level = 0.95)
head(pre)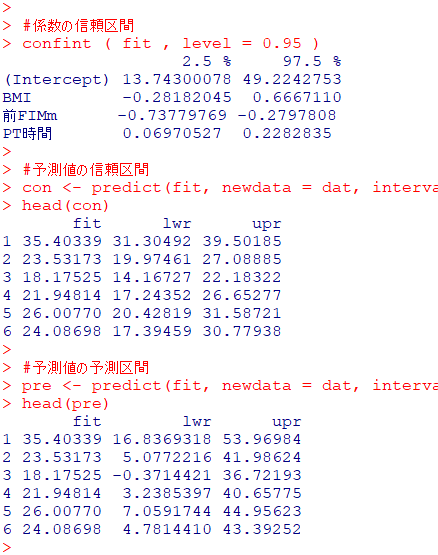

分散分析表

分散分析で詳細を説明しています

anova(fit)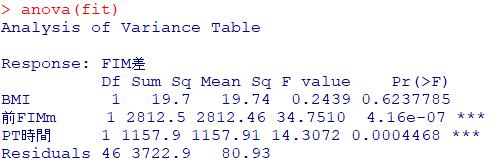

２つの表がどのような関係になっているのか確認してみましょう

残差平方和（ここではSresとします）

回帰分析の結果から求めてみます

#回帰式から得た予測値と実際の値の差の二乗和
Sres <- sum((dat$FIM差 - yhat1)^2) %>% 
print()

分散分析表（Residuals）と同じ値になります

anova(fit)$Sum[4]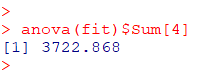

回帰モデルの平方和（ここではSregとします）

#回帰分析より
#回帰式から得た予測値と実際の値の平均値との差の二乗和
Sreg <- sum((yhat2 - mean(dat$FIM差))^2) %>% 
print()

#分散分析表も同じ値を求めることができます
#BMI, 前FIMm、PT時間のSum Sq（平方和）の総和
anova(fit)$Sum[1:3] %>% 
sum()

Residual standard error (残差の標準誤差)

回帰分析と分散分析表から求めることができます

$残差の標準誤差＝\sqrt{\dfrac{残差平方和}{自由度}}$

#回帰分析表より
#残差平方和=Sres
#残差の自由度＝サンプルサイズ-変数の数-１
Sres_df <- dim(dat)[1]-3-1

#残差の標準誤差
sqrt(Sres/Sres_df)

#分散分析表より
sqrt(anova(fit)$Sum[4]/anova(fit)$Df[4])

Multiple R-squared (決定係数)

#回帰分析の結果より
#回帰式から得た平方和=Sreg
#残差平方和 =Sres
1 - Sres / (Sreg+Sres)

#分散分析表より
全平方和 <- sum(anova(fit)$Sum)
残差平方和 <- anova(fit)$Sum[4]
1 - (残差平方和 / 全平方和)

Adjusted R-squared (自由度調整済み決定係数)

平方和を自由度で調整した決定係数

残差の変動 = 残差平方和÷自由度（サンプルサイズー変数の数ー1）
全体の変動 = 全平方和÷自由度（サンプルサイズー1）

Adjusted R-squared = $1-\dfrac{残差の変動}{全体の変動}$

#回帰式からの平方和=Sreg
#残差平方和=Sres
#残差の自由度＝Sres_df

#全平方和
Sall <- Sres + Sreg

#全平方和の自由度
df <- dim(dat)[1]-1

#Adjusted R-squared
1 - (Sres / Sres_df)/(Sall/ df)

#分散分析表より
an <- anova(fit)
1-(an$Sum[4]/an$Df[4]) / (sum(an$Sum[1:4]/df))

F値

F分布を使用して回帰式全体の検定を行う

帰無仮説：$\beta_0=\beta_1= \dotsb = \beta_j=0$

つまり帰無仮説が棄却されなければ「この回帰式は全く意味がない」ということになります

$Fvalue = \dfrac{\dfrac{Sreg}{df}}{\dfrac{Sres}{Sres\_df}}$

同じF値を求めることができます

#回帰分析より
#残差平方和＝Sres
#回帰式からの平方和=Sreg
Fvalue1 <- (Sreg/3)/(Sres/(49-3-1))
print(Fvalue1)

#分散分析表より
S0 <- sum(anova(fit)$Sum)
S1 <- anova(fit)$Sum[4]
Fvalue2 <- ((S0 - S1)/3)/(S1/(49-3-1))
print(Fvalue2)

あとはF分布に従って検定します