主成分分析(PCA：Principal Component Analysis)

主成分分析の目的
データの準備と要約
使用するパッケージ
PCAのイメージ（２変数の場合）
関数prcompを使用したPCAの実行（２変数の場合）

主成分分析の目的

主成分分析（PCA）は、高次元のデータセットをより少ない次元のデータセットに要約する統計的手法です．例えば、10変数（10次元）のデータセットを、まとめて2変数（2次元）のデータセットへの圧縮することが可能になります．PCAでは、データセットの分散が最大となる方向を見つけ出し、その方向に新たな軸（主成分）を設定します．データポイントをこの新たな軸に射影することで得られる値が主成分スコアとなります．第一主成分はデータの分散を最も大きく捉える軸であり、第二主成分は第一主成分に直交し、それに次いで分散を最大化する方向を示します．これにより、元のデータセットの重要な情報を保持しつつ次元削減が可能となります．

ここでは、変数Aと変数Bからなる二次元データを一次元（第一主成分）に要約する例を挙げて説明します．例えば、主成分は次のように表されます: 主成分 $=\beta_1$変数A$+\beta_2$変数B．ここで、$\beta_1$ と $\beta_2$ は主成分負荷量と呼ばれ、それぞれの変数が第一主成分にどのように寄与するかを示す係数です．

主成分 $=\beta_1$変数A$+\beta_2$変数B

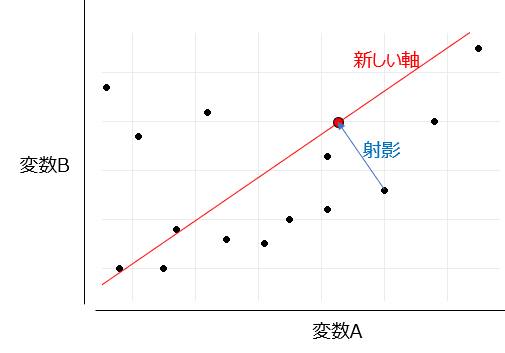
注意）３次元までは何とか視覚化できますが、４次元以上は困難です

　PCAの目的は、各変数の情報を最大限に保持しながら、射影したデータの分散が最大になる新たな軸（主成分）を探すことです．この軸上におけるデータの位置（主成分スコア）は、寄与率に応じて元の変数における変動を表します．これにより、データの次元を削減しつつ重要な情報を抽出し、解釈や分析が容易になります．

教師なし学習

PCAは回帰分析のようにあらかじめ定義された変数（目的変数）を予測することを目的としていないため、教師なし学習の一種とされています．

データの準備と要約

データセットPCA_dataをdatに格納します（ファイルの読み込み）

PCA_data サンプルデータのダウンロード

dat <- read.csv("PCA_data.csv", header=T, fileEncoding = "UTF-8")
head(dat)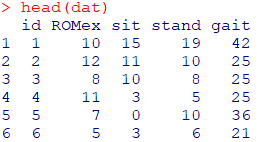

サンプルデータPCA_dataを使用して、二次元データを一次元データに圧縮するプロセスを解説します．PCA_dataには、理学療法の時間を計測したデータが記録されており、データセットには立位練習の時間（stand）と歩行練習の時間（gait）の2つの変数が含まれています．これらの変数を組み合わせてPCAを実行し、主成分スコアを求めます．この新しい変数（主成分スコア）は、standとgaitをそれぞれの負荷量に基づいて線形結合した値です．このスコアを用いることで、standとgaitの全体的なパフォーマンスを1つの尺度として表現することができます．

使用するパッケージ

使用するパッケージ（パッケージのインストール）

library(ggplot2)
library(GGally)

PCAのイメージ（２変数の場合）

PCAの結果をグラフでイメージしてみます．本来であれば多次元のデータをグラフ化すべきなのですが、イメージするためには二次元が理解しやすいので、立位練習の時間（stand）と歩行練習の時間（gait）の2変数を例にしてグラフ化します．2変数に関連があるのが視覚的に理解できます．数字はIDを示します．

# 散布図を作成し、データポイントの番号を追加
plot <- ggplot(dat, aes(x = gait, y = stand)) +
  geom_text(aes(label = seq_along(id)), vjust = 1.5, color = "red") + #id列に対して連番生成
  theme_minimal() +
  labs(title = "PCA_data",　x = "歩行の時間", y = "立位の時間") +
   theme(plot.title = element_text(hjust = 0.5)) 

# プロットを表示
print(plot)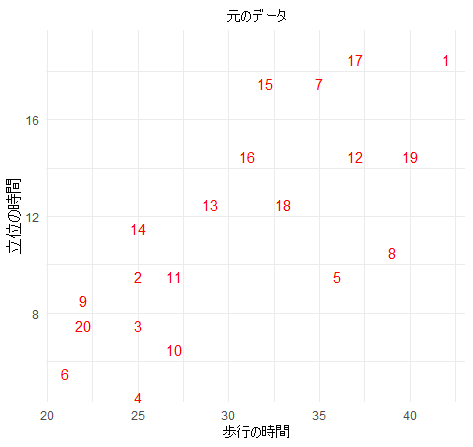

第一主成分と第二主成分のイメージは以下のようになります．分散が最大となる方向に第一主成分の軸が存在します．また、第一主成分の垂直方向に第二主成分の軸が存在します．

主成分軸が決定したら、各データを主成分軸に射影し、その値が主成分スコアとなります．

関数prcompを使用したPCAの実行（２変数の場合）

Rの関数prcomp（statsパッケージ）を使用してPCAを実行します．主成分軸を決定する方法として、相関行列に基づく方法と分散共分散行列に基づく方法があります．ここでは相関行列に基づくPCAを実行します．軸の決定方法の詳細については後述します．

#相関行列よりPCAを実行, pca_result <- prcomp(data, scale = TRUE)
data <- dat[,c("stand", "gait")]
pca_result <- prcomp(data, scale = TRUE)
summary(pca_result)

*scale=FALSEとするとデータが標準化されず、元のデータのまま使用され、分散共分散行列に基づくPCAが実行されます．

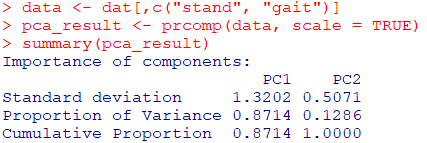
Standard deviation（標準偏差）：各主成分の標準偏差を示しており、データの分散の大きさを反映する．対応する固有値の平方根に等しく、各主成分によって説明されるデータの分散の大きさを示す．
Proportion of Variance（分散の割合）：各主成分によって説明される分散の割合を示す．各主成分の固有値を全固有値の合計で割った値．全データの分散に対する各主成分の寄与率．
Cumulative Proportion（累積分散割合）：第一主成分から順に累積した分散の割合（各主成分の固有値の累積割合）．

主成分スコア

pca_scores <- pca_result$x 
head(round(pca_scores, 3))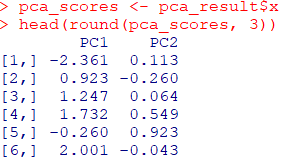

PC1の列に表示された数値が第一主成分の主成分スコアです．PC2の列は第二主成分の主成分スコアとなります．６行のみ表示しています．第一主成分（PC1）は、立位練習の時間（stand）と歩行練習の時間（gait）の分散の87.14%を説明する線形合成変数です．第二主成分（PC2）は、残りの12.86%の分散を説明します．

二次元のデータを主成分分析（PCA）により1次元に変換した結果、得られた第一主成分は、元のデータセット全体の分散の87.1%を説明します．これは、第一主成分が元のデータセットに含まれる分散の大部分を捉えることができていることを意味し、この1次元の要約が元の二次元データの重要な特徴を効果的に表現していることを示しています．

prcomp 関数で得られる rotation には、各主成分に対応する固有ベクトル（後述）が含まれています．これらの固有ベクトルは、元のデータセットの変数を新たな主成分空間に射影する際に使用されます．以下のコードで固有ベクトル（負荷量行列）を示し、各主成分における元の変数の寄与（負荷量）が確認できます。

round(pca_result$rotation, 3)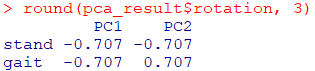

主成分スコアの求め方
scale 関数でデータを標準化します．その標準化されたデータに主成分負荷量行列を掛けることで、主成分スコアを求めることができます．scale = FALSEの場合は、データセットに直接掛けることで、主成分スコアを求めることができます．

標準化されたデータの行列　×　固有ベクトルの行列　＝　主成分スコア行列

scale(data)%*%pca_result$rotation