 分散分析
分散分析 二元配置分散分析(繰り返し測定あり)
リハビリテーション統計学では利用頻度の高い解析です。自主的に毎日体操しているA群、運動指導を受けているB群、運動指導を受けてかつ毎日自主的に体操しているAB群の肩関節屈曲可動域を計測します。肩関節屈曲可動域に年齢や運動により可動域の差はあるか、また年齢と運動の交互作用の効果について有意水準5%で検証します。
 分散分析
分散分析  2群の比較
2群の比較  分散分析
分散分析  分散分析
分散分析  分散分析
分散分析  分散分析
分散分析  分散分析
分散分析  分散分析
分散分析 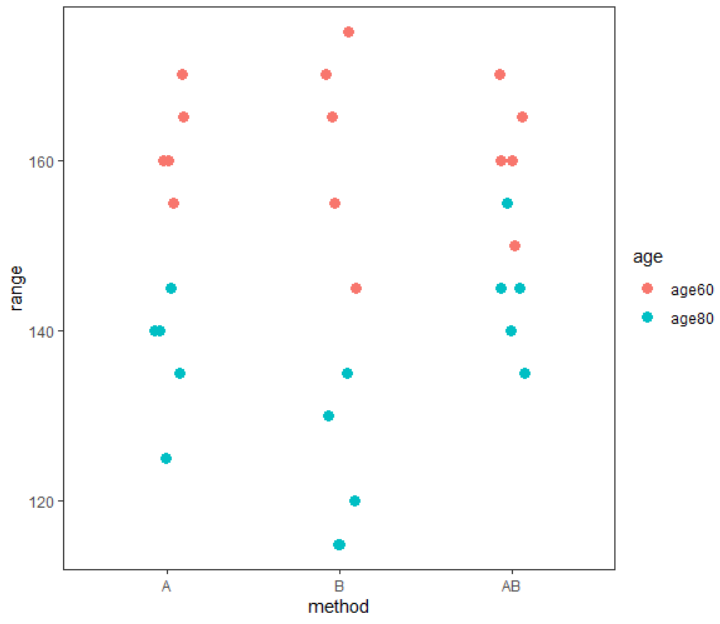 グラフ
グラフ  分散分析
分散分析