 定理・公式
定理・公式 中心極限定理
リハビリテーション統計学の基礎理論となる中心極限定理について解説しています。
 定理・公式
定理・公式  Rの関数
Rの関数  備忘録
備忘録  備忘録
備忘録  回帰分析
回帰分析  分散分析
分散分析  備忘録
備忘録  2群の比較
2群の比較  備忘録
備忘録  回帰分析
回帰分析  2群の比較
2群の比較 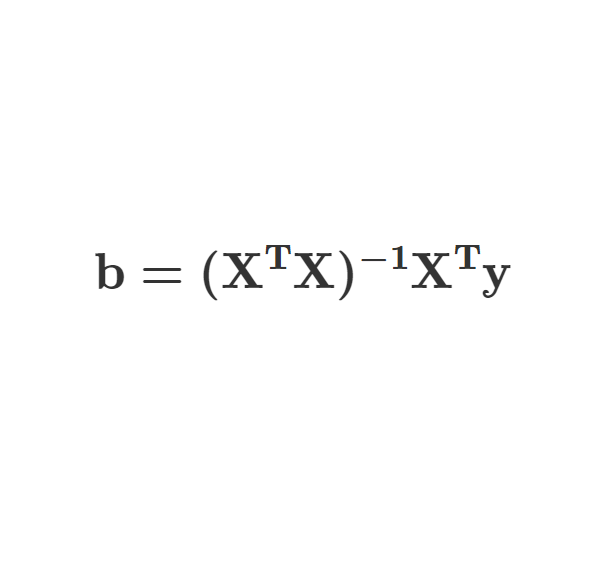 回帰分析
回帰分析  分散分析
分散分析  備忘録
備忘録  グラフ
グラフ  分散分析
分散分析