Rで作る分割表（クロス表）

効果の有無で層別
コクラン-マンテル-ヘンツェル検定で共通オッズ比の検定
リスク比、オッズ比
基準の変更

効果の有無で層別

歩行練習の有無で層別

tab2 <- xtabs( ~ musc + effect + gait, data = dat)
print(tab2)

> print(tab2)
, , gait = no

     effect
musc  good not
  no     2   8
  yes    3   3

, , gait = yes

     effect
musc  good not
  no     4   1
  yes    9   0

コクラン-マンテル-ヘンツェル検定で共通オッズ比の検定

mantelhaen.test()関数を用いて、マンテル・ヘンゼル検定を実施します。この検定は、複数の層にわたる2×2分割表に対して、層別化されたオッズ比の均一性を評価するものです。この検定により、筋肉訓練の有無、歩行訓練の有無を考慮しつつ、治療効果（「good」vs「not」）の独立性を評価します。この分析により、歩行練習の有無によって層別された状況下での治療効果の関連性が評価され、調整後のリスク比やオッズ比が得られます。これにより、歩行練習が治療効果に与える影響の強さと方向を、他の変数の影響を調整しながら解析することが可能になります。

mantelhaen.test(tab2)

> mantelhaen.test(tab2) 

        Mantel-Haenszel chi-squared test with continuity correction

data:  tab2
Mantel-Haenszel X-squared = 1.4761, df = 1, p-value = 0.2244
alternative hypothesis: true common odds ratio is not equal to 1
95 percent confidence interval:
 0.02148238 1.42558684
sample estimates:
common odds ratio 
            0.175

効果＝有効のみの分割表

tab3 <- xtabs(
    ~ musc + effect, 
    data=dat[dat$gait=="yes",] 
)
print(tab3)

> print(tab3)
     effect
musc  good not
  no     4   1
  yes    9   0

リスク比、オッズ比

例）治療あり群が転倒するリスクを調査します（ここでは暴露＝治療となります）
treat : 治療あり
no treat : 治療なし
falls : 転倒あり
no falls : 転倒なし

tab4 <- matrix(c(3, 9, 12, 6), 2, 2)
rownames(tab4) <- c("treat", "no treat")
colnames(tab4) <- c("falls", "no falls")
print(tab4)

> print(tab4)
         falls no falls
treat        3       12
no treat     9        6

パッケージ mgcv を使用します（パッケージのインストール）

library(mgcv) 
Epi::twoby2(tab4)

> Epi::twoby2(tab4)
2 by 2 table analysis: 
------------------------------------------------------ 
Outcome   : falls 
Comparing : treat vs. no treat 

         falls no falls    P(falls) 95% conf. interval
treat        3       12         0.2    0.0659   0.4698
no treat     9        6         0.6    0.3481   0.8082

                                    95% conf. interval
             Relative Risk:  0.3333    0.1117   0.9946
         Sample Odds Ratio:  0.1667    0.0325   0.8535
Conditional MLE Odds Ratio:  0.1781    0.0223   1.0612
    Probability difference: -0.4000   -0.6398  -0.0504

             Exact P-value: 0.0604 
        Asymptotic P-value: 0.0315 
------------------------------------------------------

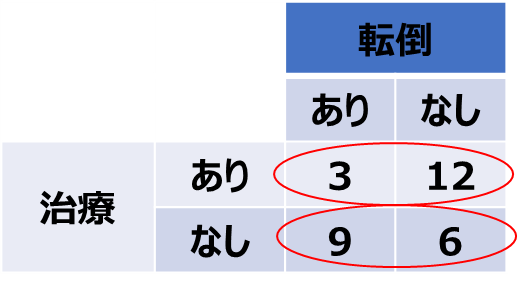
Relative Risk: 相対リスク（二つのグループのリスクの比率、リスク＝暴露群が転倒するリスク）

相対リスク$=\dfrac{3}{15} /\dfrac{9}{15}$

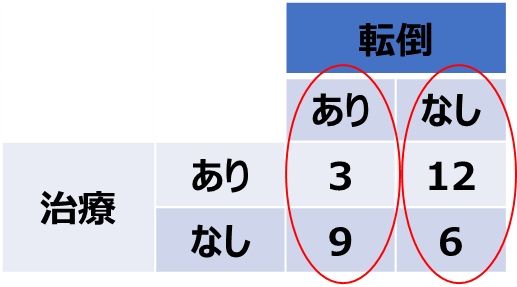
Sample Odds Ratio: オッズ比（二つのグループのオッズの比率、オッズ＝暴露割合/非暴露割合）

後ろ向き研究の場合を想定して、暴露オッズ比を求めます

オッズ比$=\dfrac{3}{9} /\dfrac{12}{6}$

Conditional MLE Odds Ratio: 条件付き最尤推定（MLE）オッズ比

Probability difference: 治療「あり」と「なし」グループで効果「有効」のアウトカムが発生する確率の差

確率差$=\dfrac{3}{15}-/\dfrac{9}{15}$

後ろ向きケース・コントロール研究ではリスクが計算できません。
そのためオッズ比を計算して関連性を検証します！
比を求める場合は、分母がコントロール群となります！！！

基準の変更

ロジスティック回帰で基準を変更する場合

dat$effect_n <- ifelse(dat$effect=="good", 1 , 0)
fit <- glm(
    formula = effect_n ~ musc + gait,
    family = binomial,
    data = dat
)
summary(fit)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)   
(Intercept)  -1.5609     0.7914  -1.972  0.04858 * 
muscyes       1.7379     1.0468   1.660  0.09685 . 
gaityes       3.3190     1.2351   2.687  0.00721 **

歩行練習（gait）は有意になりました。歩行練習なしに比べると、歩行練習あり群のオッズは$e^3.319=27.6$倍になることが推定されました。

関数 reveal を使用して歩行練習の基準カテゴリーを”yes”に変更してみます。基準を操作する場合には、変数をfactorに変更します。

dat$gait <- factor(dat$gait)
dat$gait_2 <- relevel(dat$gait, ref="yes")
fit2 <- glm(
    formula = effect_n ~ gait_2 + musc,
    family = binomial,
    data = dat
)
summary(fit2)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)   
(Intercept)    1.758      1.106   1.589  0.11199   
gait_2no      -3.319      1.235  -2.687  0.00721 **
muscyes        1.738      1.047   1.660  0.09685 .

gaitの結果がマイナスに転じていることが確認できます。