合併した分散（併合分散, プールした分散）
２群の分散が同じだと仮定した場合（等分散）
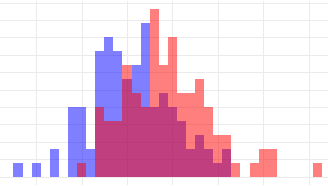
対応のある2群の平均値は1標本の問題となるので、シンプルな分散でした（対応のあるｔ検定）．もし両群の分散（\(\sigma^2\)）が既知であったならば、分散の加法性よりZ値は以下のようになります．
X群の平均を\(\bar{X}\)、Y群の平均を\(\bar{Y}\)
X群の母平均を\(\mu_x\)、Y群の母平均を\(\mu_y\)
X群のサンプルサイズを\(n_x\)、Y群のサンプルサイズを\(n_y\)
\(Z=\dfrac{(\bar{X} – \bar{Y})-(\mu_x – \mu_y)}{\sqrt{\dfrac{\sigma^2}{n_x}+\dfrac{\sigma^2}{n_y}}} \, \sim N(0, \, 1)\)
ただし、\(\sigma^2\) は未知なので、それぞれの不偏分散 \(\hat{s_x}^2\)、\(\hat{s_y}^2\)に置き換えなければなりません
t分布より
\(t=\dfrac{Z}{\sqrt{\dfrac{W}{k}}} \, \sim t(k)\)
この \(W\) は自由度 \(k\) の \(\chi^2\) 分布です
X, Yの母集団は正規分布であるため、カイ二乗分布の性質より以下のことが成り立ちます（ここがポイント）
\(\chi_X^2=\dfrac{\Sigma{(X_i-\bar{X})^2}}{\sigma^2}\,\sim\chi(n_X\,-\,1)\)
\(\chi_Y^2=\dfrac{\Sigma{(Y_i-\bar{Y})^2}}{\sigma^2}\,\sim\chi(n_Y\,-\,1)\)
\(w=\chi_X^2 \, + \, \chi_Y^2\)とするとｶｲ二乗分布の再生性より
\(w = \dfrac{(n_x-1)s_X^2+(n_y-1)s_Y^2}{\sigma^2} \, \sim\chi(n_x + n_y-2)\)
これで\(\sigma^2\) を不偏分散$\hat{s_x}^2、\hat{s_y}^2$に置き換えることができます
\(\sigma^2=\dfrac{(n_x-1)\hat{s_x}^2+(n_y-1)\hat{s_y}^2}{w}\)
これまでの結果から \(T\) は自由度\(n_x+n_y-2\)のｔ分布に従います
\(T=\dfrac{Z}{\sqrt{(\dfrac{w}{n_x+n_y-2})}}\)
\(Z\) と \(w\) を上式に当てはめると以下のようになります
\(T=\dfrac{(\bar{X} – \bar{Y})-(\mu_x – \mu_y)}{\sqrt{\dfrac{\sigma^2}{n_x}+\dfrac{\sigma^2}{n_y}}}\sqrt{\dfrac{\sigma^2(n_x+n_y-2)}{(n_x-1)\hat{s_x}^2+(n_y-1)\hat{s_y}^2}}\)
\(=\dfrac{(\bar{X} – \bar{Y})-(\mu_x – \mu_y)}{s^2\sqrt{\dfrac{1}{n_x}+\dfrac{1}{n_y}}}\)
\(s^2=\dfrac{(n_x-1)\hat{s_x}^2+(n_y-1)\hat{s_x}^2}{n_x+n_y-2}\)・・・これが合併した分散
これでｔ値を求めることができます。サンプルデータを当てはめてみましょう！
t値
s2 <- ((28-1)*9.7^2 + (31-1)*8.57^2)/(28+31-2)
(t <- (25.1-30.7)/(sqrt(s2*(1/28+1/31))))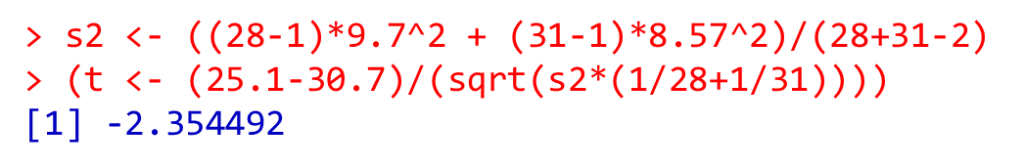
データセットから標準偏差と平均を求める方法
sx <- sd(dat_long[dat_long$group=="X", "data"])
sy <- sd(dat_long[dat_long$group=="Y","data"])
mx <- mean(dat_long[dat_long$group=="X", "data"])
my <- mean(dat_long[dat_long$group=="Y", "data"])
s2 <- ((28 - 1)*sx^2 + (31 - 1)*sy^2)/(28 + 31 - 2)
(t <- (mx - my)/(sqrt(s2*(1/28 + 1/31))))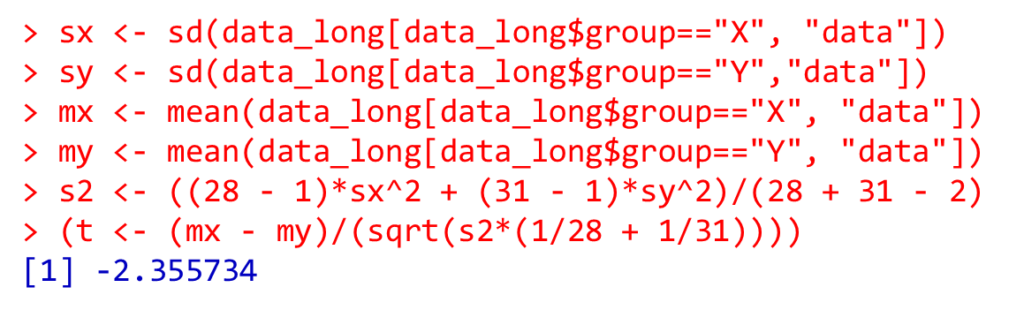
２群の分散が異なると仮定した場合は、Welchの検定の適用になります
RでWelchの検定を実行
t.test(data~group, var.equal=FALSE, data=dat_long)
◆ ｔ値＝-2.3408の求め方
$\hat{s_X}^2$ と $\hat{s_Y}^2$ が等しいと想定できな場合は、次のようにｔ統計量を定義します
$T=\dfrac{\bar{x}-\bar{y}}{\sqrt{\dfrac{\hat{s_x}^2}{n_x}+\dfrac{\hat{s_x}^2}{n_y}}}$
自由度は以下のようになります（整数になるとは限りません）
$d_1=\dfrac{\hat{s_x}^2}{n_x}$、$d_1=\dfrac{\hat{s_y}^2}{n_y}$
$df = \dfrac{(d_1+d_2)^2}{\dfrac{d_1^2}{n_x-1}+\dfrac{d_2^2}{n_y-1}}$
◆ 実際の数値を代入してみましょう
自由度
d1 <- 9.696656^2/28
d2 <- 8.572023^2/31
df <- (d1+d2)^2/((d1^2/(28-1))+(d2^2/(31-1)))
print(df)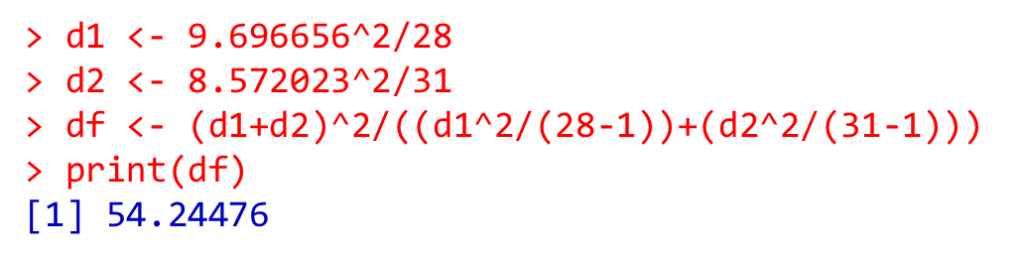
ｔ値
t <- (25.10714-30.70968)/sqrt(d1+d2)
print(t)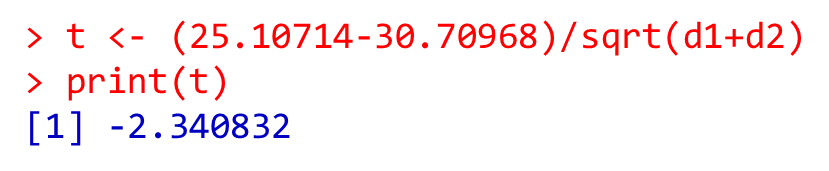
p値
pt(-2.340832, 54.24476)*2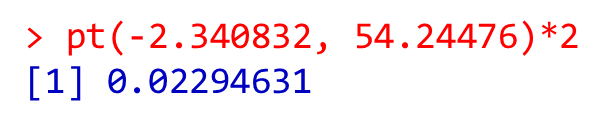
検定方法
結果の解釈については対応のあるｔ検定をご確認ください
コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください