共分散分析, ANCOVA, アンコバ

1ページ　2ページ

非並行性の検定（交互性の検定）

各群の回帰直線

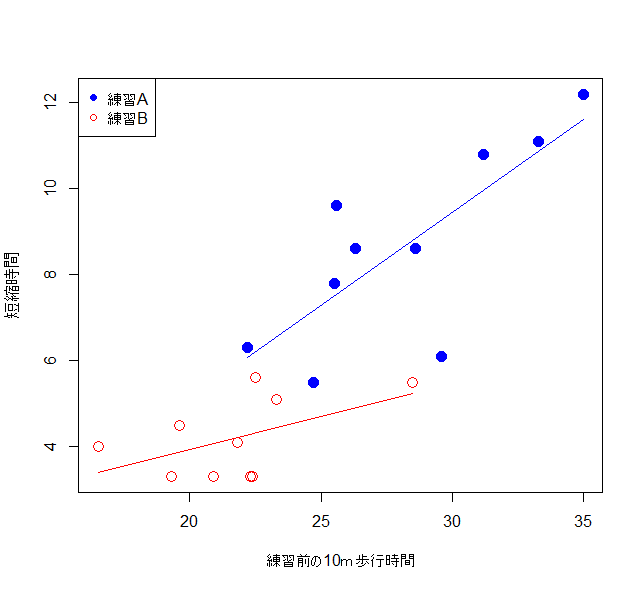
非平行性の検定のp値が大きい場合には、両群の回帰直線の傾きが非並行ということになります。両群の共通回帰直線は無意味になり、それぞれの回帰式を吟味しなければなりません。

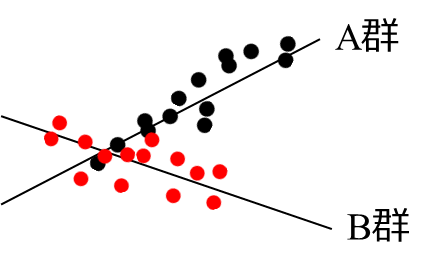
非平行性の検定のp値が小さい場合には、両群の回帰直線の傾きが並行ということになります。この場合には共通する傾きを利用した回帰直線で検証することとなります。

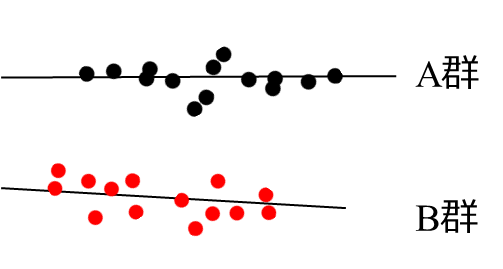
回帰分析と分散分析で並行性を検定してみます

fit2 <- lm(short ~ gait * pre,  data=data)
summary(fit2)

> summary(fit2)

Call:
lm(formula = short ~ gait * pre, data = data)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.1653 -0.5919  0.2472  0.6316  2.0641 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -3.5320     2.8928  -1.221 0.239776    
gaitB         4.4047     4.0947   1.076 0.298011    
pre           0.4323     0.1016   4.254 0.000606 ***
gaitB:pre    -0.2791     0.1668  -1.673 0.113726    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.242 on 16 degrees of freedom
Multiple R-squared:  0.8399,    Adjusted R-squared:  0.8099 
F-statistic: 27.98 on 3 and 16 DF,  p-value: 1.334e-06

p>0.05という結果になり交互作用は有意ではありません

この結果から歩行練習Aと歩行練習Bの回帰直線を求めることができます
歩行練習Aの切片$=-3.532$
歩行練習Bの切片$=-3.532+4.4047=0.8727$
歩行練習Aの傾き$=0.4323$
歩行練習Bの傾き$＝0.4323-0.2791=0.1532$

結果
歩行練習A$=-3.532+0.4323*$歩行練習前の10ｍ歩行時間
歩行練習B$=0.8727+0.1532*$歩行練習前の10ｍ歩行時間

注意）回帰直線は描けますが、外挿の予測はできません（結果を求めた標本の範囲内の予測のみ）

anova(fit2)

> anova(fit2)
Analysis of Variance Table

Response: short
          Df Sum Sq Mean Sq F value    Pr(>F)    
gait       1 99.458  99.458 64.5044  5.27e-07 ***
pre        1 25.657  25.657 16.6403 0.0008738 ***
gait:pre   1  4.317   4.317  2.7996 0.1137261    
Residuals 16 24.670   1.542                      
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

もちろん同じｐ値になりますが、p>0.05という結果になり交互作用は有意ではありません（この検定結果で両群の回帰直線が非平行性を決める場合もあります）。交互作用項の平均平方和は各群の回帰式と共通する傾きをもつ回帰式の推定値から求めることができます（詳細は省略しますが、参考図のみ載せておきます）。

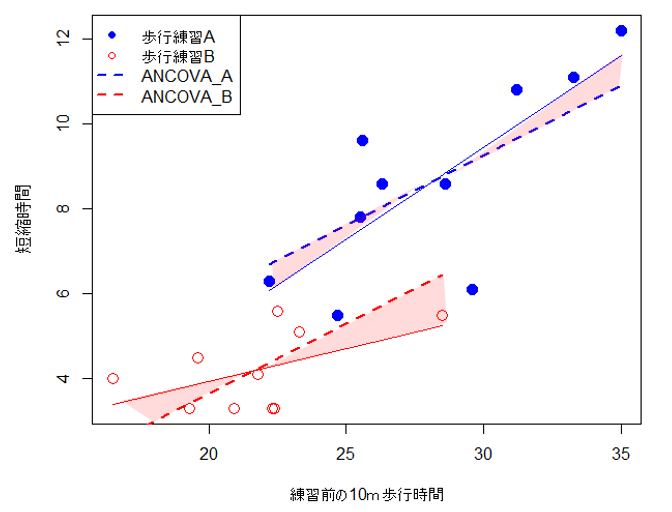
参考

両群に共通した回帰直線を求めるために以下のような作業を行います

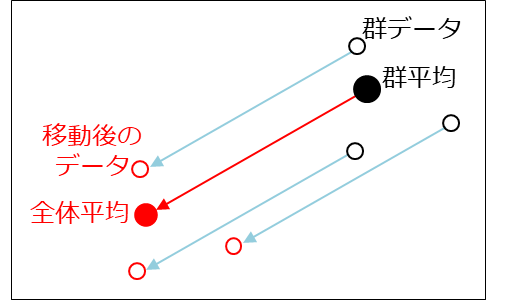
まず歩行練習A群の平均を全体の平均までの移動させます（→）。次に、データを同じ距離を平行移動させます（→）。歩行練習B群も同じ操作を行い、全て移行させたデータから求めた回帰直線の傾きが共通した傾きとなります。

共通回帰の検定

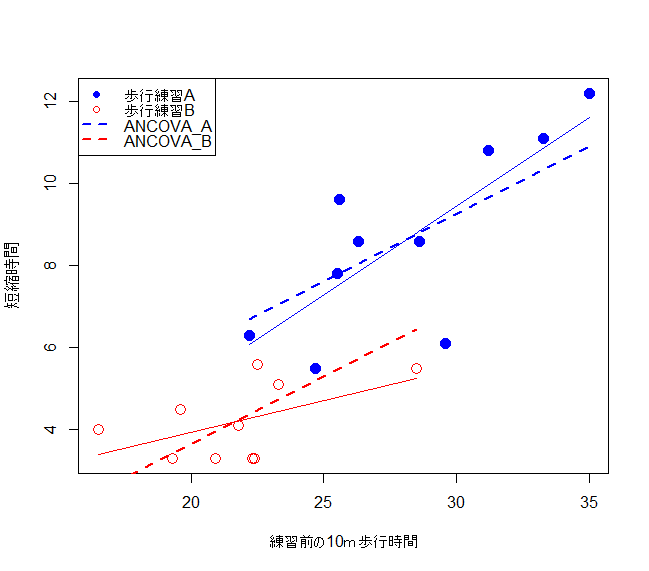
交互作用項が有意ではなかったので、共通回帰直線（点線）が意味をもつかどうかを検定します。群間で共通の傾き（共通回帰直線）を使用することが妥当である、という統計的な検証になります。

summary(fit)

> summary(fit)

Call:
lm(formula = short ~ gait + pre, data = data)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.0202 -0.7083 -0.0401  1.0303  1.7947 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) -0.61018    2.42519  -0.252  0.80436   
gaitB       -2.32654    0.80219  -2.900  0.00996 **
pre          0.32873    0.08474   3.879  0.00121 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.306 on 17 degrees of freedom
Multiple R-squared:  0.8119,    Adjusted R-squared:  0.7898 
F-statistic: 36.69 on 2 and 17 DF,  p-value: 6.797e-07

この統計モデルにおけるF値は36.69であり、対応するp値は0.05未満（具体的には6.797e-07）で、これによりモデル全体が統計的に有意であることが確認されます。これは、モデルに含まれる予測因子が目的変数である歩行時間の短縮に対して有意な説明を提供していることを示しています。特に、「pre」変数（練習前の10m歩行時間）のp値は0.00121で、これは練習前の10m歩行時間が歩行時間の短縮に正の影響を与えていることを示しています。この結果から、練習前の10m歩行時間は、歩行時間の短縮を予測する際の重要な因子として考慮すべきであると結論付けることができます。

F値の求め方（詳細は重回帰分析をご覧ください）

各群の共通回帰（赤と青の点線）から得られる推定値と各群の平均値との差の平均平方和を残差の平均平方和で除したF値で検定します（平方和については分散分析、重回帰分析で解説してます）。共通回帰のF値が大きければ共通回帰が意味を持つことになります。小さい場合には、共通回帰の傾きが0に近いことを意味します。

# Predicted values of reduction time obtained from covariance analysis (fit)
yhat <- predict(fit)
# Sum of squares of the differences between the predicted values from the regression equation and the actual mean values
Sreg <- sum((yhat - mean(data$short))^2)
# Sum of squared residuals
Sres <- sum((yhat - data$short)^2)
# F-value = (Sreg/degrees of freedom) ÷ (Sres/degrees of freedom)
F <- (Sreg/2) / (Sres / (20 - 2 - 1))
print(F)
# F-test
pf(F, 2, 17, lower.tail=FALSE)

> print(F)
[1] 36.68865
> # F-test
> pf(F, 2, 17, lower.tail=FALSE)
[1] 6.796902e-07

共分散分析の結果と同じ値になりました

参考（いつもお世話になってます）

統計学入門−第8章

www.snap-tck.com