正規性の検定

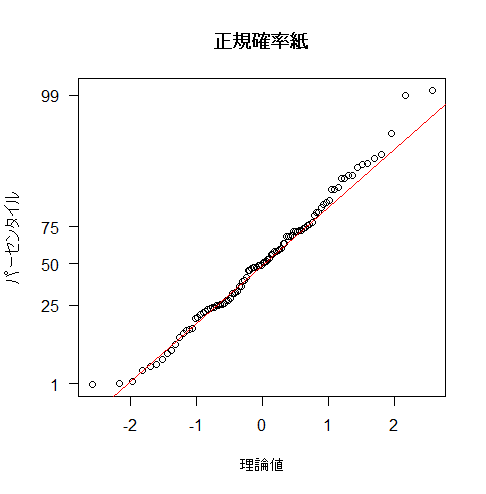
データの準備と要約

使用するパッケージ（パッケージのインストール）

library(ggplot2)
library(dplyr)

データセット unif をdatに格納します（ファイルの読み込み）.

サンプルデータの取り込み

setwd("C:\\Users\\rehay\\Documents\\back up folder\\統計学備忘録\\ブログで使用したサンプル")
getwd()
.libPaths("C:\\Users\\rehay\\Documents\\Rpackages")

dat <- read.csv("unif.csv", header=T, fileEncoding = "UTF-8")
head(dat)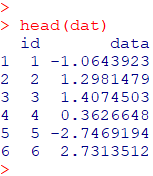

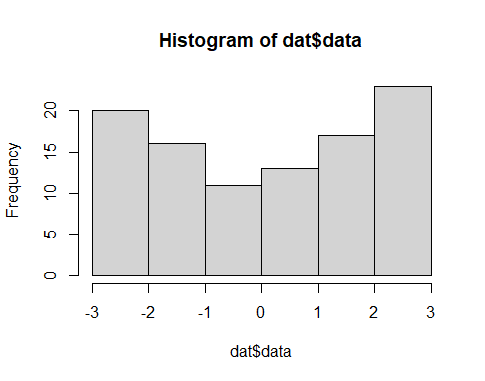
hist(dat$data)

サンプルデータの unif は一様分布からの乱数です

検定

データセット unif についてKolmogorov-Smirnov 検定（コルモゴロフ・スミルノフ検定）とShapiro-Wilk検定を実行します。

帰無仮説：サンプルデータは指定された理論分布（ここでは正規分布）に従う
有意水準：5％

1標本のKolmogorov-Smirnov 検定（KS検定）

y=”pnorm” で正規分布を指定します

 ks.test(
  x=dat$data, y="pnorm",
  mean=mean(dat$data),
  sd=sd(dat$data)
)

p>0.05より、データが正規分布に従うという帰無仮説を棄却するには十分ではありません。従って「サンプルデータは正規分布から有意に逸脱しているとは言えない」という結果になりました。

Shapiro-Wilk検定

shapiro.test(x=dat$data)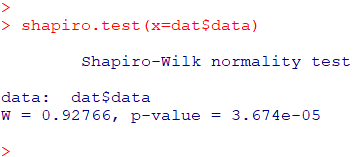

p<0.05より、データが正規分布に従うという帰無仮説が棄却されます。従って「サンプルデータは正規分布から有意に逸脱している」と考えられます。

Kolmogorov-Smirnov検定とShapiro-Wilk検定では判定が異なります。ヒストグラムを見た限りでは、正規分布ではないようですので、Shapiro-Wilk検定が正しいようです。

Q-Qプロット（正規性の評価）

X軸には理論分布の分位数（Theoretical Quantile）を、Y軸にはデータの分位数（Sample Quantiles）を表示します。選択した理論分布にどの程度従っているかを視覚的に評価します。

y2pt.com

2024.03.17