 回帰分析
回帰分析 ロジスティック回帰 (1)
リハビリテーション統計学で利用頻度の高い線形回帰モデルです。リハビリを受けている入院中の患者に対してリハビリに関する満足度調査を実施した。1週間に割り当てられた単位数をもとにランダムにインタビューした。「満足」と回答する割合と1週間のリハビリ単位数には関係があるのでしょうか?
 回帰分析
回帰分析  2群の比較
2群の比較  回帰分析
回帰分析 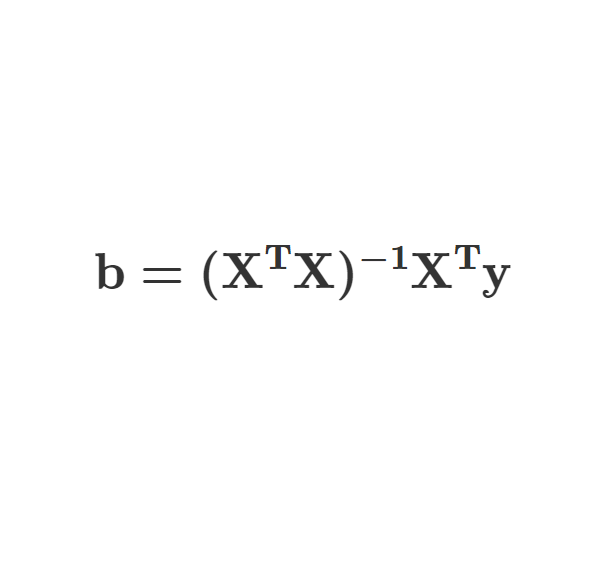 回帰分析
回帰分析  回帰分析
回帰分析  分散分析
分散分析  回帰分析
回帰分析  回帰分析
回帰分析  回帰分析
回帰分析 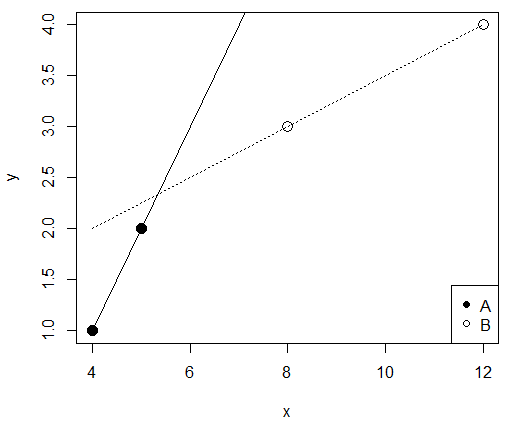 グラフ
グラフ 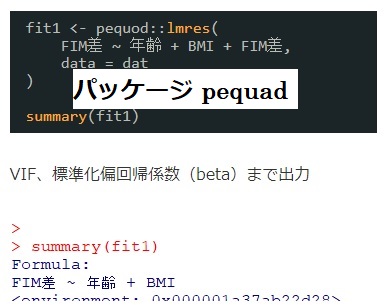 回帰分析
回帰分析