 グラフ
グラフ データを可視化する
リハビリテーション統計学にデータの可視化は必須です。脳卒中片麻痺患者Aさんの血圧測定結果を考えてみます。Aさんは高血圧の既往があります。でも皆さんご存じのとおり、個人内変動があります。1週間(月曜日~土曜日)PT前後に血圧を測定した場合の結果です。日常的な臨床記録で見かける1週間で蓄積したデータを統計学的に考えてみます。
 グラフ
グラフ 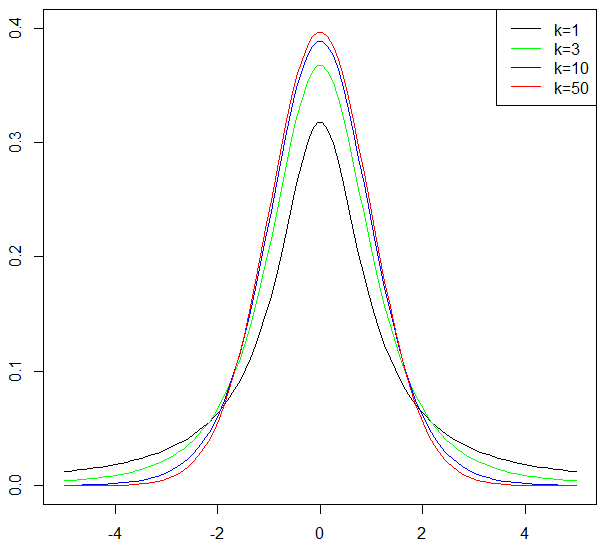 確率分布
確率分布  確率分布
確率分布  確率分布
確率分布  確率分布
確率分布 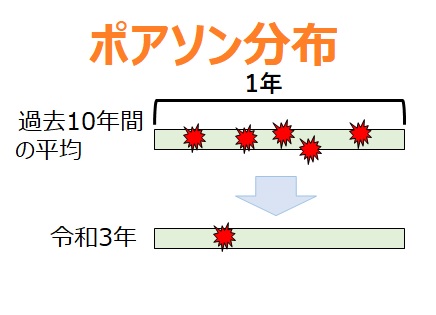 確率分布
確率分布  2群の比較
2群の比較  確率分布
確率分布  グラフ
グラフ