 グラフ
グラフ ROC曲線
罹患の有無を判定するために、あるテストの感度と特異度を調べます。感度と特異度からROC曲線を描きます。またROC曲線よりカットオフ値を求めます。
 グラフ
グラフ  備忘録
備忘録  回帰分析
回帰分析 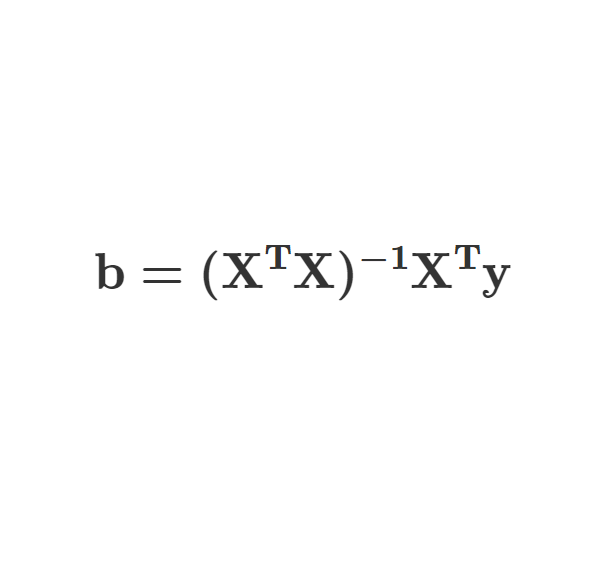 回帰分析
回帰分析  回帰分析
回帰分析  グラフ
グラフ  分散分析
分散分析  回帰分析
回帰分析 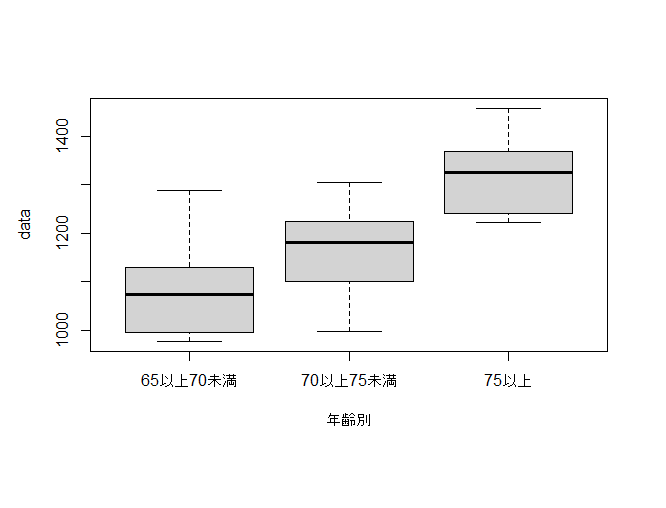 備忘録
備忘録  備忘録
備忘録 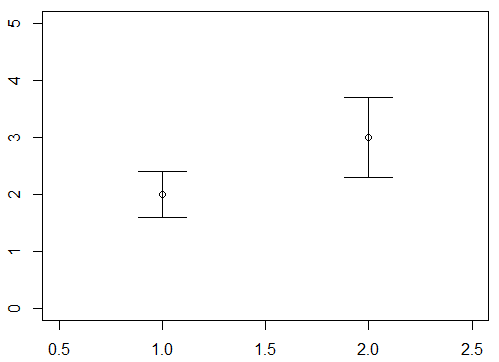 グラフ
グラフ 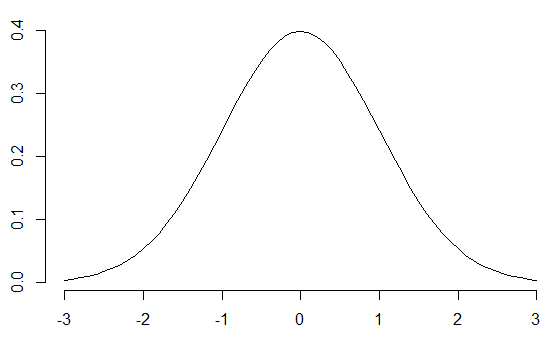 グラフ
グラフ 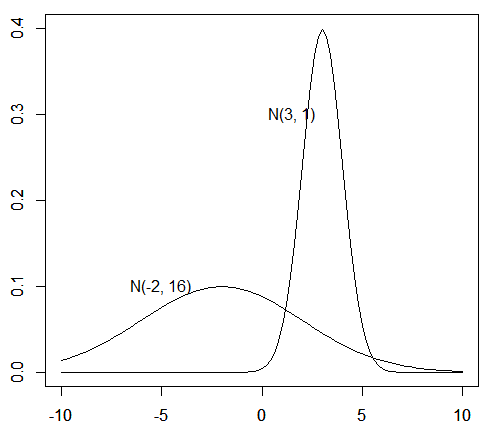 グラフ
グラフ 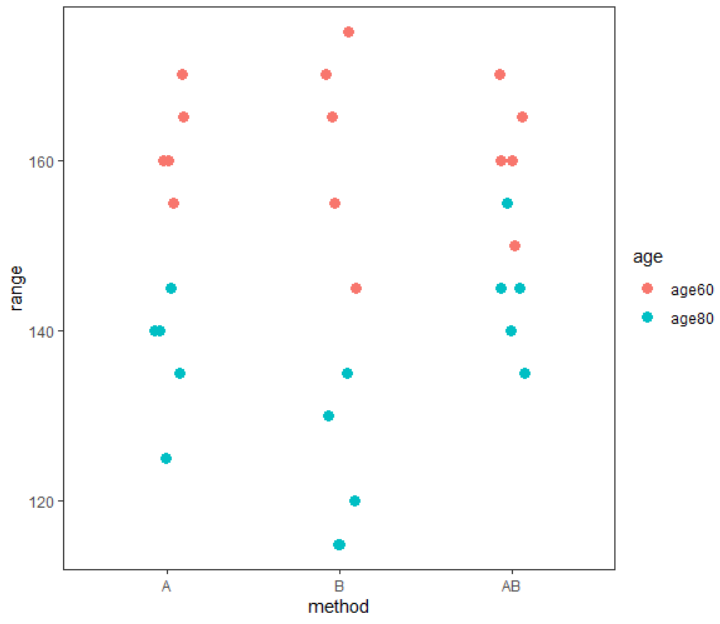 グラフ
グラフ 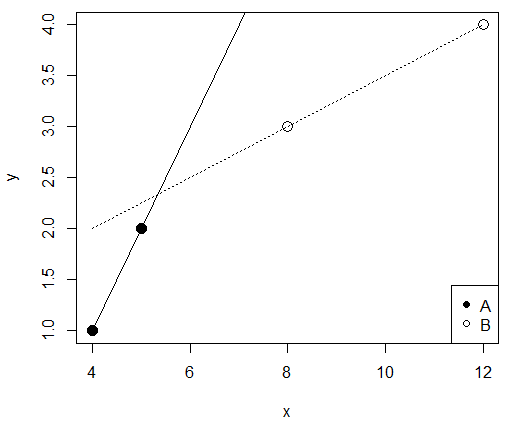 グラフ
グラフ  定理・公式
定理・公式